Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 71

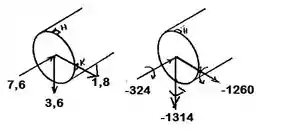
Para o sistema do Prob 5.70 determinar as tensões, normal e de cisalhamento, no ponto K.

Passo 1

Do enunciado temos

d i n t = 68   m m

d e x t = 80   m m

Com isso podemos calcular A, J e I.

A = π 0,0 4 2 - 0,034 2 = 1,39 × 10 - 3 m 2

J = π 2 0,04 4 - 0,034 4 = 1,92 × 10 - 6 m 4

I = π c 4 4 = π × 0,04 4 4 - π × 0,034 4 4 = 9 , 61 × 10 - 7 m 4

Passo 2

Vamos agora decompor a força F em seus respectivos eixos

F z = F × 0,38 0,38 + 0,18 + 0,09 = 8,6 × 0,38 0,38 + 0,18 + 0,09 = 7,6   k N

F x = 8,6 × 0,09 0,38 + 0,18 + 0,09 = 1,8   k N

F y = 8,6 × 0,18 0,38 + 0,18 + 0,09 = 3,6   k N

Esses são os valores da força agora presentes no ponto B

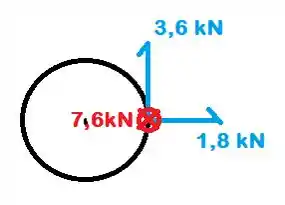
Passo 3

Fazendo agora uma análise das forças teremos

P = - 7,6   k N

V y = 3,6   k N

V x = 1,8   k N

M x = - 0,35 × 3600 = - 1260   N . m

M y = 0,09 × 7600 + 0,35 × 1800 = 1314   N . m

M z = 0,09 × 3600 = 324   N . m

Passo 4

Com essas informações spodemos comçar a calcular as tensões normal e de cisalhamento no ponto H

Calculando o Q

Q = 2 3 c 3 = 2 3 × 40 3 = 42667   m m 3

σ K = P A - M y c I = - 7,6 1,39 × 10 - 3 - 1314 × 0,04 9,61 × 10 - 7 = - 5 4693   M P a

τ K = M z c J + V Q I t = 324 × 0,04 1,92 × 10 - 6 + 3600 × 42667 × 10 - 9 9,61 × 10 - 7 × 0,08 = 8747,9   M P a  

Resposta

σ K = - 54693   M P a

τ K = 8747,9   M P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga é composta por quatro tábuas coladas ao longo das linhas de junção. Se a cola puder resistir a 15 kN/m e a viga sofrer uma rotação de 90°, qual é o cisalhamento vertical máximo V que a viga pod
A viga é composta por quatro tábuas coladas ao longo das linhas de junção. Se a cola puder resistir a 15 kN/m, qual é o cisalhamento vertical máximo V que a viga pode suportar?
O elemento está sujeito a uma força de cisalhamento V = 2 kN. Determine o fluxo de cisalhamento máximo no elemento. Todos os segmentos da seção transversal têm 15 mm de espessura.
Uma chapa de aço com espessura 6 mm é dobrada para formar a seção de paredes finas mostrada na figura. Se for submetida a uma força de cisalhamento V = 1,25 kN, determine a tensão de cisalhamento no p
O elemento está sujeito a uma força de cisalhamento V = 2 kN. Determine o fluxo de cisalhamento nos pontos A, B e C. A espessura de cada segmento de paredes finas é 15 mm.