Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 70

A barra AB é conectada, através de juntas esféricas, ao colar A ao disco de raio 90 mm. O disco é soldado ao tubo DE, que tem um diâmetro externo de 80 mm e uma espessura igual a 6 mm. Sabendo-se que na posição mostrada a barra AB está comprimida e exerce uma força de 8,6 kN, no ponto B, determinar as tensões normal e de cisalhamento, no ponto H.

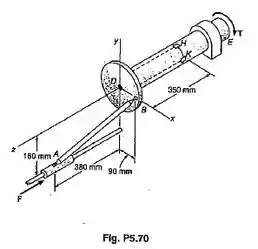
Passo 1

Do enunciado temos

d i n t = 68   m m

d e x t = 80   m m

Com isso podemos calcular A, J e I.

A = π 0,0 4 2 - 0,034 2 = 1,39 × 10 - 3 m 2

J = π 2 0,04 4 - 0,034 4 = 1,92 × 10 - 6 m 4

I = π c 4 4 = π × 0,04 4 4 - π × 0,034 4 4 = 9 , 61 × 10 - 7 m 4

Passo 2

Vamos agora decompor a força F em seus respectivos eixos

F z = F × 0,38 0,38 + 0,18 + 0,09 = 8,6 × 0,38 0,38 + 0,18 + 0,09 = 7,6   k N

F x = 8,6 × 0,09 0,38 + 0,18 + 0,09 = 1,8   k N

F y = 8,6 × 0,18 0,38 + 0,18 + 0,09 = 3,6   k N

Esses são os valores da força agora presentes no ponto B

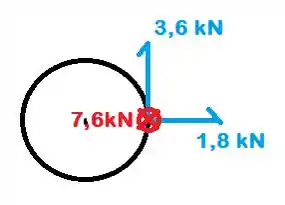
Passo 3

Fazendo agora uma análise das forças teremos

P = - 7,6   k N

V y = 3,6   k N

V x = 1,8   k N

M x = - 0,35 × 3600 = - 1260   N . m

M y = 0,09 × 7600 + 0,35 × 1800 = 1314   N . m

M z = 0,09 × 3600 = 324   N . m

Passo 4

Com essas informações spodemos comçar a calcular as tensões normal e de cisalhamento no ponto H

Calculando o Q

Q = 2 3 c 3 = 2 3 × 40 3 = 42667   m m 3

σ H = P A - M x c I = - 7,6 1,39 × 10 - 3 + 1260 × 0,04 9,61 × 10 - 7 = 52440   M P a

τ H = M z c J = 324 × 0,04 1,92 × 10 - 6 = 6750   M P a  

Resposta

σ H = 52440   M P a

τ H = 6750   M P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga na na Figura 6.54f é submetida a um momento totalmente plástico Mp. Prove que as tensões de cisalhamento longitudinal e transversal na viga são nulas. Dica: Considere um elemento da viga como m
A viga de madeira T está sujeita a uma carga composta por n forças concentradas, P N . Se a tensão de cisalhamento admissível V p r e g o para cada um dos pregos for conhecida, escreva um código compu
Uma viga de madeira é composta por n tábuas, cada uma com seção transversal retangular. Escreva um código computacional que possa ser usado para determinar a tensão de cisalhamento máxima na viga quan
A viga tem seção transversal retangular e está sujeita a uma carga P cuja intensidade é suficiente para desenvolver um momento totalmente plástico M P = P L no apoio fixo. Se o material for elástico-p
Uma chapa de aço com espessura 6 mm é dobrada para formar a seção de paredes finas mostrada na figura. Se for submetida a uma força de cisalhamento V = 1,25 kN, determine a tensão de cisalhamento nos