Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 1

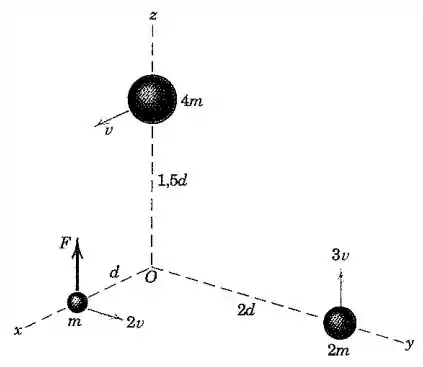
O sistema de três partículas possui as massas, velocidades e forças externas indicadas nas partículas. Determine r - , r - ˙ , r - ¨ , T , H O e H O ˙ para esse sistema.

Passo 1

Vamos lembrar que a posição do centro de massa é calculada assim:

  r - = ∑ m i r i ∑ m i

r - = m d   i + 2 m 2 d   j + 4 m 1,5 d   k m + 2 m + 4 m

r - = d 7 ( i + 4   j + 6   k )

Já a velocidade do centro de massa por ser obtida derivando a expressão da posição em relação ao tempo:

r - = ∑ m i r i ∑ m i

r - ˙ = ∑ m i r i ˙ ∑ m i

r - ˙ = m 2 v   j + 2 m 3 v   k + 4 m v   i 7 m

r - ˙ = v 7 ( 4   i + 2   j + 6   k )

Passo 2

Para calcular a aceleração do centro de massa, usaremos a Segunda Lei de Newton Generalizada:

∑ F = ∑ m i r - ¨

r - ¨ = ∑ F ∑ m i

Como a única força externa tem módulo F e age para cima, temos:

r - ¨ = F   k 7 m

Mas lembre-se de que a energia cinética total do sistema é uma grandeza escalar, sendo ela a soma das energias cinéticas de cada partícula, beleza?

T = ∑ 1 2 m i v i 2 = 1 2 m 2 v 2 + 1 2 2 m 3 v 2 + 1 2 4 m v 2

T = 13 m v 2

Passo 3

Show! Agora vamos calcular a quantidade de movimento angular em relação à origem:

H O = ∑ r i × m i v i

H O = d   i × m 2 v   j + 2 d   j × 2 m 3 v   k + 1,5 d   k × 4 m v   i

H O = 2 m v d   ( i × j ) + 12 m v d   ( j × k ) + 6 m v d   k × i

H O = 2 m v d   k + 12 m v d   i + 6 m v d   j

H O = m v d   ( 12   i + 6   j + 2   k )

Por último, lembre-se de que a derivada da quantidade de movimento angular é a somatória dos momentos:

H O ˙ = ∑ M o

H O ˙ = ∑ r i × F i

H O ˙ = d   i × F   k

H O ˙ = F d   i × k

H O ˙ = - F d   j

Resposta

r - = d 7 ( i + 4   j + 6   k )

r - ˙ = v 7 ( 4   i + 2   j + 6   k )

r - ¨ = F   k 7 m

T = 13 m v 2

H O = m v d   ( 12   i + 6   j + 2   k )

H O ˙ = - F d   j

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O salto triplo é uma prova do atletismo em que o atleta faz uma corrida de arrancada e tenta se projetar o mais longe possível com um salto inicial, dois passos e um salto final. A figura mostra o sal
O projeto para uma nova prótese de quadril está sendo estudado usando um instrumento de inserção e um fêmur fixo falso. Considerando que o punção aplica uma força média de 2 kN durante um tempo de 2 m
A última parte da prova de salto triplo do atletismo é o salto final, em que o atleta faz o último salto e aterrissa em uma caixa de areia. Considerando que a velocidade de um atleta de 90 kg justamen
O seguinte modelo matemático foi sugerido para a variação na pressão dentro do diâmetro de 10 mm do cano de um rifle quando uma bala de 25 g é disparada: p t = 950M P a e - t / ( 0,16m s ) onde t é ex
Uma estimativa da carga esperada sobre cintos de segurança é feita antes de se desenhar protótipos de cintos que serão avaliados em testes de impacto com automóveis. Admitindo que um automóvel que rod