Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 75
A solda em pode suportar uma força máxima de ao longo de cada uma das direções e e um momento máximo de . Determine a faixa admissível para a direçao da força de aplicada em . O ângulo está restrito a .
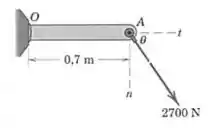
Passo 1
Bom, nós sabemos que o momento da força em relação a se deve totalmente ao componente dessa força que é perpendicular à barra , certo? Então vamos escrever essa expressão:
E as componentes das forças em e também são fáceis de escrever:
Passo 2
E agora ficamos apenas com um problema matemático! Queremos achar uma faixa de valores para que satisfazem todas as seguintes relações:
E se isolarmos as funções trigonométricas:
E podemos excluir a última exigência para o seno, já que a primeira necessariamente já satisfaz a última:
Agora é só resolver essas duas inequações, lembrando que o seno é uma função crescente no intervalo e o cosseno é decrescente. Então:
E então o intervalo admissível é:
Resposta
A faixa admissível é .