O suporte está preso à coluna por meio de dois rebites, e , e suporta uma força de . Substitua essa força por uma força atuando ao longo da mediatriz dos rebites e por um binário. Em seguida, redistribua essa força e o binário, substituindo-os por duas forças, uma em e outra em , e determine as forças suportadas pelos rebites.
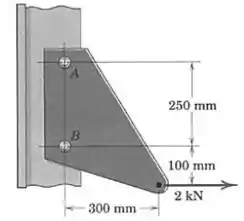
Passo 1
Vamos fazer o procedimento de sempre para substituir a força por um sistema força-binário equivalente: deslocar a força para outro ponto, e calcular o momento da força original em relação ao novo ponto:
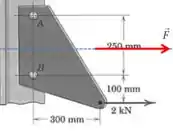
Passo 2
Vamos continuar seguindo os passos sugeridos pelo enunciado: agora temos que dividir essa força de em duas outras forças aplicadas nos pontos e :
Ok, isso já cumpre o papel da força , mas e o binário? Ainda precisamos aplicar mais forças nos pontos e para produzir um binário de no mesmo sentido do original (anti-horário).
Como a distância entre os pontos de aplicação das duas forças é , podemos calcular o módulo da força em cada ponto usando essa equação:
E para que essas forças produzam momento no sentido anti-horário, a situação deve ser a seguinte:
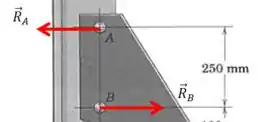
Passo 3
Agora já podemos calcular a força total em cada um dos pontos:
E os módulos das forças são e .
Resposta
Os módulos das forças em e são e , respectivamente.