Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 74
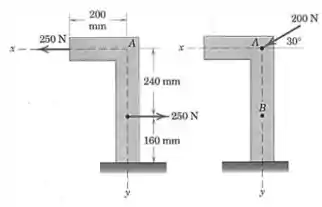
A placa dobrada está submetida às duas forças de mostradas. Deseja-se substituir essas forças por um conjunto equivalente formado pela força de aplicada em e uma segunda força aplicada em . Determine a coordenada de .
Passo 1
Na figura da esquerda, as duas forças aplicadas sobre a placa tinham o mesmo módulo e direção, mas sentidos opostos. Isso quer dizer que elas formam um par binário, e podemos calcular o momento associado a ele usando a seguinte equação:
Isso quer dizer que, se o nosso novo par de forças será equivalente a esse, precisamos manter esse mesmo resultado.
Passo 2
Assim como antes, a força aplicada em deve ter a mesma direção e módulo da aplicada em , mas com sentidos opostos.
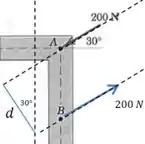
E todo o nosso objetivo é descobrir a coordenada do ponto onde a nossa força será aplicada. Então vamos começar calculando :
E agora a relação entre e pode ser tirada diretamente do nosso desenho:
Resposta
A coordenada do ponto é .