Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 99

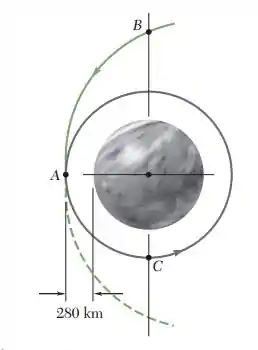
Quando uma sonda espacial, que se aproxima do planeta Vênus em uma trajetória parabólica, atinge o ponto A mais próximo do planeta, sua velocidade é diminuída para que ela seja inserida em uma órbita circular. Sabendo que a massa e o raio de Vênus são 4,87   ×   10 24 kge 6.052 km, respectivamente, determine: (a) a velocidade da sonda quando ela se aproxima de A, (b) a diminuição da velocidade necessária para inseri-la em uma órbita circular.

Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente determine a velocidade da sonda quando ela se aproxima de A, (b) a diminuição da velocidade necessária para inseri-la em uma órbita circular. Então vem comigo :D

Primeira nota: r A = 6052   + 280 k m = 6332   k m

(a) A velocidade no ponto de aproximação mais próxima em uma trajetória parabólica é dada por:

v 0 =   2 G M r 0

Portanto, ( v A ) p a r = [ 2   × 66.73   ×   10 - 12   m ³ K g ∙   s 2 × 4.87   ×   10 24   K g 6332   ×   10 3 m ] 1 / 2 = 10,131.4   m / s

Passo 2

(b)Temos: ( v A ) c i r c = ( v A ) p a r + ∆ v A

Agora: ( v A ) c i r c = G M r 0 = 1 2 = ( v A ) p a r

Então temos que a velocidade é dada por:

∆ v A = 1 2 ( v A ) p a r - ( v A ) p a r = 1 2 - 1   ( 10.1314   K m / s = - 2.97   K m / s

Resposta

  1. ( v A ) p a r = 10.13   K m / s

  2. ∆ v A = 2.97   K m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento de uma partícula é definido pelas equações x = ( 2 t + t 2 ) m e y = ( t 2 ) m, onde t é dado em segundos. Determine as componentes normal e tangencial da velocidade e aceleração da partíc
As partículas A e B estão se deslocando em torno de uma pista circular a uma velocidade escalar de 8 m/s no instante mostrado. Se a velocidade escalar de B está aumentando na razão de a t B = 4m / s 2
Uma bola é chutada com velocidade escalar inicial v A = 8m / s a um ângulo θ A = 40 ° com a horizontal. Encontre a equação da trajetória, y = f ( x ) , e, em seguida, determine as componentes normal e
Dois ciclistas, A e B, estão se deslocando no sentido anti-horário em torno de uma pista circular a uma velocidade escalar constante de 2,4m / s no instante mostrado. Se a velocidade escalar de A é au
As partículas A e B estão se deslocando no sentido anti-horário em torno de uma pista circular a uma velocidade escalar constante de 8m / s . Se no instante mostrado a velocidade de A é aumentada na r