Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 117
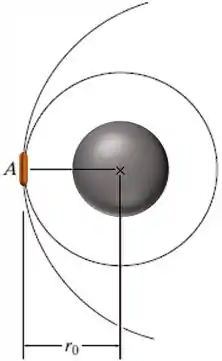
A sonda Viking aproxima-se do planeta Marte em uma trajetória parabólica, como mostrado. Quando ele alcança o ponto , sua velocidade é de 10 Mm/h. Determine e a velocidade necessária em de maneira que ele possa manter uma órbita circular, como mostrado. A massa de Marte é 0,1074 vezes a massa da Terra.
Passo 1
O enunciando nos informa que:
A trajetória é parabólica;
Velocidade da sonda em :
Massa de Marte:
E pede para determinarmos Determine e a velocidade necessária em de maneira que a sonda possa manter uma órbita circular.
Suponha que o raio da Terra é 6378 km;
A massa da Terra é de 5,976(1024) kg;
A massa do Sol é de ,99(1030) kg;
A constante gravitacional é de .
Vamos tranformar de para , que é a unidade utilizada em geral.
Passo 2
Quando a sonda Viking alcança o ponto através de uma trajetória parabólica, sua velocidade no ponto é dada por
Passo 3
Quando a sonda viaja através de uma trajetória circular onde , sua velocidade é dada por