Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 123

Se o foguete deve pousar na superfície do planeta, determine a velocidade escalar de voo livre que ele deve ter em A ' de maneira que o pouso ocorra em B . Quanto tempo o foguete leva para pousar, indo de A ' para B ? O planeta não tem atmosfera, e sua massa é 0,6 vezes a da Terra.

Passo 1

O enunciado nos diz que:

A massa do planeta é de M P = 0,6   M e e seu raio é de r = 3200   k m ;

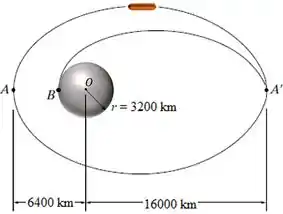
Além disso, analisando a imagem, podemos ver que se trata de uma órbita elíptica.

O foguete está em uma órbita elíptica inicial e quando chega em A ' deve entrar em uma segunda órbita elíptica com ponto final em B .

Devemos definir a velocidade vetorial do foguete no ponto A ' para que ele pouse em B e o tempo necessário para este movimento.

Suponha que o raio da Terra é 6378 km;

A massa da Terra é de M e = 5,976(1024) kg;

A massa do Sol é de M s = 1 ,99(1030) kg;

A constante gravitacional é de G = 66,73 10 - 12   m 3 / ( k g   s 2 ) .

Raio da Terra: r T = 6378   k m

Passo 2

Analisando somente a segunda rota elíptica, que é do nosso interesse, vemos que o raio do perigeu ( r p ) e do apogeu ( r a ) da órbita são dados por

r p = O B = 3200   k m

r a = O A ' = 16000   k m

Além disso, sabemos que M P = 0,6   M e , logo

M P = 0,6 5,976 10 24 = 3,5856 10 24   k g

Com estes dados, podemos utilizar a fórmula que relaciona o raio de apogeu e do perigeu com a velocidade vetorial do perigeu para encontrar a velocidade no ponto B .

r a = r P 2 G M P r P v P 2 - 1

O A ' = O B 2 G M P O B v B 2 - 1

Colocando v B em evidência, temos

v B = 2 G M P O B O B O A ' + 1 = 2 ( 66,73 ) 10 - 12 3,59 10 24 3200 ( 10 3 ) 3200 16000 + 1

v B = 11163,26   m / s

Passo 3

A constante h é dada por

h = r v

logo,

h = O B v B = O A ' v A '

3200 ( 10 3 ) ( 11163,26 ) = 16000 ( 10 3 ) v A '

v A ' = 2232,65   m / s

v A ' = 2 , 23   k m / s

Passo 4

Agora que já sabemos a velocidade, vamos encontrar o período T para obtermos o tempo que o foguete leva para pousar no ponto B .

Sabemos que

T = π h r p + r a r p r a

E

h = O B v B = 3,57 ( 10 10 )

Logo,

T = π h 3200 ( 10 3 ) + 16000 ( 10 3 ) ( 3200 ) ( 10 3 ) ( 16000 ) ( 10 3 )

T = 12089,77   s

O período T representa o período de tempo necessário para fazer uma revolução orbital. Ao analisar a imagem, vemos que o trajetória elíptica A ’ B é metade de uma revolução, portanto

t = T 2 = 6044,88   s

t = 1,679   h

Resposta

v A ' = 2,23   k m / s

t = 1,679   h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um veículo é projetado para combinar a sensação de uma motocicleta com o conforto e a segurança de um automóvel. Se o veículo está se movendo a uma velocidade constante de 80 km/h ao longo de uma estr
Determine o coeficiente de atrito estático entre os pneus e a superfície da estrada é μ s = 0,25 , determine a velocidade máxima do carro de 1,5 Mg de modo que ele não deslize quando ele se move na cu
Um avião de 5 Mg está voando com uma velocidade constante de 350 km/h ao longo da trajetória circular horizontal. Se o ângulo de inclinação θ = 15 ° , determine a força de sustentação L atuando sobre
Um bloco liso B, tendo massa de 0,2 kg, está ligado ao vértice A do cone circular reto utilizando uma corda leve. Se o bloco tem velocidade de 0,5 m/s em torno do cone, determine a tração na corda e a
Se a bola tem massa de 30k g e uma velocidade de v = 4m / s no instante em que ela está no ponto mais baixo, θ = 0 ° . Determine a tração da corda e a taxa na qual a velocidade da bola está desacelera