Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 79
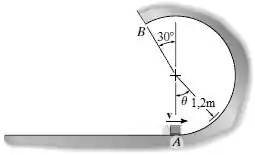
Determine a velocidde mínima que deve ser dada à caixa de 2,5 kg em a fim de que ela permaneça em contato com a trajetória circular. Determine também a velocidade da caixa quando ela chega ao ponto .
Passo 1
O enunciado nos dá as seguintes informações:
Massa da caixa: 2,5 kg;
Pista circular: trajetória curva;
Raio: m.
Nosso objetivo é determinar a velocidade mínima da caixa em para que ela não desgrude da pista durante sua trajetória. Em seguida, determinaremos a velocidade da caixa quando no ponto
Primeiramente, desenharemos o Diagrama de Corpo Livre da caixa.
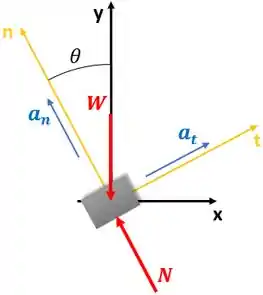
Onde = força peso
= força normal resultante
= aceleração tangencial
=aceleração normal
Lembre-se que a aceleração normal deve apontar no sentido positivo do eixo normal . Como a aceleração tangencial é desconhecida, vamos supor que ela atue na direção de positiva.
Sabemos que m/s2 e que
Passo 2
Agora, utilizaremos as Equações do Movimento.
Aplicando a Equação do Movimento no sentindo do eixo , temos
Aplicando a Equação do Movimento no sentindo do eixo , temos
Passo 3
Sabemos que, pela relação da cinemática,
Logo,
Portanto, devemos estabeler uma relação entre e o ângulo para conseguir resolver a questão. Utilizando a relação geométrica , onde , temos que
Finalmente temos a relação
Esta é uma EDO homogênea linear de 1o ordem. Utilizaremos a condição inicial onde para para resolver a EDO.
Passo 4
Em sabemos que o bloco atinge o ponto mais alto. Nesta posição, o bloco está na iminência de cair, ou seja, está perdendo contato com a pista. Com isso, a força normal tende a zero e podemos considerá-la nula . Substituindo esses dois valores na seguinte equação de movimento, teremos
Sabemos que . Substituindo estes valores na equação da velocidade, temos
Passo 5
Agora vamos analisar o ponto . Neste ponto temos . Substituindo na equação da velocidade