Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 119
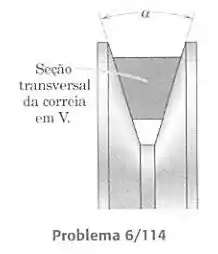
Substitua a correia plana e a polia da Fig. 6/11 por uma correia e uma polia em V, como indicado na vista da seção transversal que acompanha esse problema. Obtenha a relação entre as forças trativas na correia, o ângulo de contato e o coeficiente de atrito para a correia em V quando o movimento é iminente. O projeto de uma correia em V com seria equivalente a aumentar o coeficiente de atrito por que fator em relação a uma correia plana do mesmo material?
Passo 1
Vamos isolar uma pequena parte da correia, de angulação . Se temos uma força normal aplicada em cada lado na correia, teremos também forças de atrito aplicadas, sendo o coeficiente de atrito entre a correia e a polia. Vamos olhar para a parte da correia paralelamente à correia, para mostrar o ângulo .
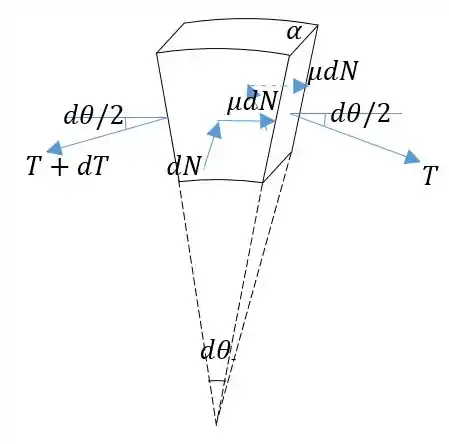
Como podemos ver, temos de um lado uma tração e do outro uma tração . O atrito irá se opor a esse acréscimo da tração. Primeiro vamos fazer a equação de equilíbrio na direção paralela ao atrito. Temos:
O cosseno de um ângulo infinitesimal pode ser considerado igual a 1, então nossa equação fica:
Passo 2
Agora fazemos o equilíbrio na direção vertical. Temos as forças normais , que têm inclinação de em relação à horizontal, e as trações, com inclinação :
O seno de um ângulo infinitesimal pode ser interpretado como o próprio ângulo. O termo pode ser ignorado, pois é um infinitesimal de ordem 2. Então:
Passo 3
Substituindo da equação na , temos:
Isolamos os termos que contém , e integramos dos dois lados:
Sendo a angulação total de giro na correia.
Passo 4
Para uma correia em com angulação de , temos a relação:
Se a correia fosse plana, a relação seria:
Então trocar a correia por uma de angulação de é equivalente a trocar por um material de com coeficiente de atrito aumentado de um fator .