Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 57

54- O hemisfério sólido de diâmetro 2 b e o cilindro concêntrico de diâmetro b estão em repouso sobre uma superfície horizontal. Determine a altura máxima h que o cilindro pode ter sem fazer com que o conjunto seja instável na posição vertical mostrada. Ambas as partes são feitas do mesmo material.

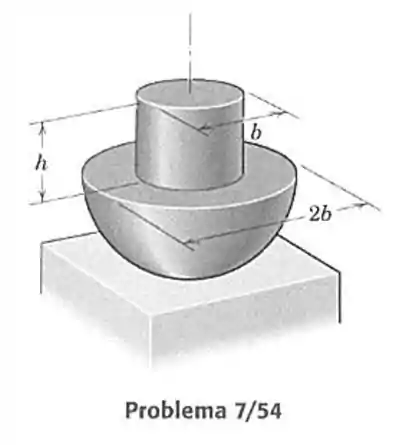
Passo 1

Precisamos de um requisito das aulas de cálculo para resolver essa questão, precisamos saber que o centroide de uma semiesfera a partir de seu centro, tal como na figura abaixo.

G = 3 r 8

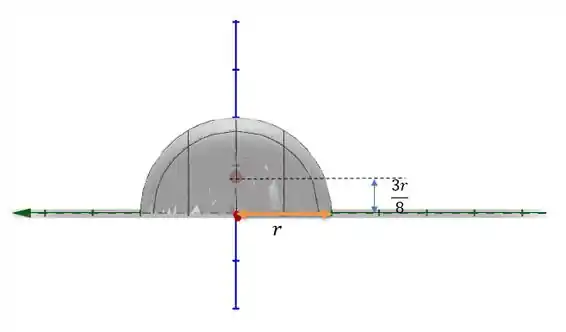
E a do cilindro será exatamente no centro dos eixos x , y e z não tendo muitos problemas em saber.

Passo 2

Vamos traçar o eixo de energia potencial gravitacional do sistema na junção entre os dois sólidos de modo que se virarmos um pouquinho o conjunto em θ nós teremos a seguinte imagem:

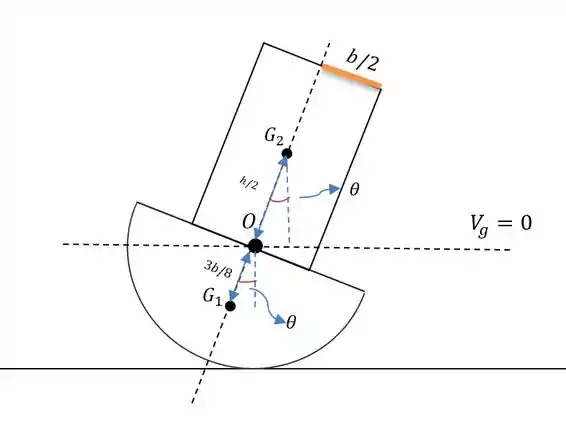
Chamaremos de sólido 1 a semicircunferência e o sólido 2 o cilindro.

Em relação ao eixo nulo e a θ a semicircunferência 1 terá altura do centro de gravidade igual a linha tracejada azul na figura que tem comprimento de:

h 1 = - 3 b 8 cos ⁡ θ

Logo a energia potencial nesse sistema será desse sólido será de:

V g 1 = - m 1 g 3 b 8 cos ⁡ θ

Já a altura do centro de gravidade do sólido 2 terá o mesmo tamanho da linha tracejada azul presente nesse sólido que será de:

h 2 = h 2 cos ⁡ θ

O que dá uma energia potencial gravitacional igual a:

V g 2 = m 2 g h 2 cos ⁡ θ

Logo a energia potencial gravitacional desse sistema será de:

V = - 3 m 1 b g 8 cos ⁡ θ + m 2 h g 2 cos ⁡ θ

Passo 3

Porém não podemos escrever as massas desses objetos dessa forma, pois eles não estão especificados com nenhuma variável que conhecemos. Porém como eles são feitos do mesmo material então eles tem a mesma densidade ρ tal que podemos escrever a massa desses sólidos da seguinte maneira.

ρ = m 1 V 1 → m 1 = ρ V 1

Da mesma forma:

m 2 = ρ V 2

Logo a energia potencial do sistema fica da seguinte maneira:

V = - 3 ρ V 1 b g 8 cos ⁡ θ + ρ V 2 h g 2 cos ⁡ θ

O volume do sólido 1 pode ser calculado da seguinte maneira:

V s e m i e s f e r a = 4 3 π r 3 2 = 2 3 π r 3

V 1 = 2 3 × π b 3

E o volume do sólido 2 :

V c i l i n d r o = π r 2 h

V 2 = π b 2 2 h = π b 2 h 4

O que deixa a energia potencial do sólido da seguinte maneira :

V = - 3 ρ b g 8 × 2 3 π b 3 cos ⁡ θ + ρ g h 2 × π b 2 h 4 cos ⁡ θ

V = ρ π b 2 h 2 g 8 cos ⁡ θ - ρ π b 4 g 4 cos ⁡ θ

V = ρ π b 2 g 4 h 2 2 - b 2 cos ⁡ θ

Passo 4

Derivando duas vezes essa equação em relação a θ nós teremos:

d 2 V d θ 2 = - ρ π b 2 g 4 h 2 2 - b 2 cos ⁡ θ

Para esse sistema ser estável nós temos que fazer:

d 2 V d θ 2 > 0

Dessa forma 0 ≤ θ ≤ π / 2 e

- h 2 2 - b 2 > 0

Já que ρ , b ,   π   e g são constantes maiores que zero.

Logo:

h 2 2 < b 2

h 2 < 2 b 2

h < b 2

Resposta

h < b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A haste uniforme A D tem 20k g de massa. Se a mola conectada não está deformada quando θ = 90 ° , determine o ângulo θ para haver equilíbrio. Observe que a mola sempre permanece na posição vertical, e
Cada elemento tem uma massa por comprimento m 0 . Determine os ângulos θ e ϕ nos quais eles estão suspensos em equilíbrio. O contato em A é liso, e ambos são conectados por um pino em B .
Determine o ângulo θ para haver equilíbrio e investigue a estabilidade nessa posição. As hastes possuem massa de 3k g cada uma e o bloco suspenso D tem massa de 7k g . A corda D C tem comprimento tota
A haste uniforme tem massa de 100k g . Se a mola não estiver deformada quando θ = 60 ° , determine o ângulo θ para haver equilíbrio e investigue a estabilidade na posição de equilíbrio. A mola sempre
O bloco triangular de peso W se apoia sobre os cantos lisos que estão separados por uma distância a . Se o bloco possui três lados iguais de comprimento d , determine o ângulo θ para que haja equilíbr