Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 187
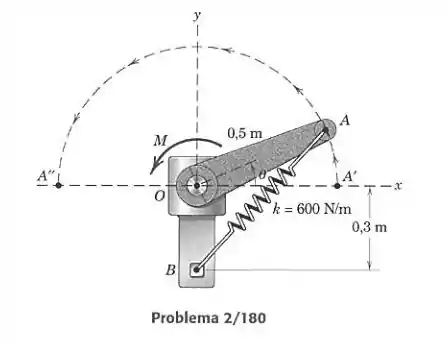
Um motor, preso ao eixo faz o braço girar na faixa ao braço. O comprimento original da mola é de 0,65 m e ela pode suportar tato tração quanto compressão. Se o momento resultante em torno de deve ser nulo, determine o torque necessário ao motor e faça um gráfico em função de .
Passo 1
Nesse exercício devemos obter a expressão vetorial da força causada pela mola no ponto , para então calcularmos o momento em torno de que essa força gera. Primeiro vamos obter o módulo da força da mola em função de sua deformação e depois obter o momento causado sabendo a posição do ponto e a direção de .
Passo 2
Primeiro vamos definir a posição do ponto . Temos a seguinte expressão:
A partir disso, temos o vetor que liga a mola ao ponto :
Passo 3
Pra acharmos o módulo da força elástica, que vem da fórmula onde é a deformação da mola, precisamos do comprimento total da mola, que é o módulo do vetor .
Então a força elástica será:
Aqui pode ser negativo, o que significa que a mola está esticada (força apontada para ) e não comprimida (força apontada de para ).
Passo 4
Agora que já temos , precisamos das projeções nas direções e para podermos calcular o momento. A força de tração tem a mesma direção que o vetor , que é dada pelo vetor unitário calculado a seguir:
Agora temos a expressão de :
Passo 5
Podemos então finalmente calcular o torque:
Resolvendo o produto vetorial, chegamos ao resultado:
E então para compensar o torque do motor deve ser:
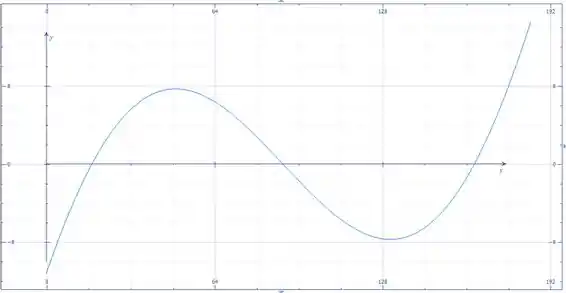
Abaixo vemos o gráfico de em função de :
