Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 104
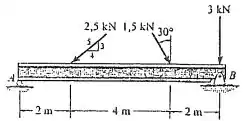
Substitua o sistema de forças que age sobre a viga por uma força e momento de binário resultante no ponto .
Passo 1
O problema pede para substituirmos o sistema de forças apresentado por uma força resultante e um momento de binário equivalente no ponto .
O que a gente vai fazer aqui é achar a força resultante e o momento resultante em . E para isso precisamos calcular a soma vetorial das forças e dos momentos.
É basicamente isso que vamos fazer. Bora lá!
Passo 2
Precisamos escrever as forças que agem sobre o sistema.
Vamos escrever na forma vetorial porque aí é mais tranquilo calcular a resultante. A força de só está no eixo e para baixo. Logo ela fica assim:
A força de faz um ângulo de graus com a vertical. Por isso, a achar a componente vertical multiplicamos a força por cosseno e a componente horizontal por seno.
Repara que a componente de cosseno é negativa porque a força aponta para baixo. Para achar as componentes de usamos o triângulo que aparece ali:
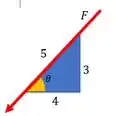
Ambas são negativas porque as forças apontam para trás e para baixo respectivamente.
A força resultante então será
Assim,
Logo,
Passo 3
Agora precisamos calcular os momentos de cada uma dessas forças com relação ao ponto . Sabemos que o momento de uma força é dado por
Assim, precisamos escrever o vetor posição de cada força relativo ao ponto . Para achar esses caras, a gente coloca a origem dos nossos eixos em . Aí o vetor para cada força vai ser a coordenada do ponto de aplicação dela menos a coordenada de .
Isso gera um vetor que começa no ponto de aplicação da força e vai até . Para a força e :
Para a força de :
Para a força de :
Assim, vamos ter
Somando todos os momentos: