88. Dois binários agem sobre a estrutura. Se o momento de binário resultante deve ser zero, determine a distância entre as forças do binário de .
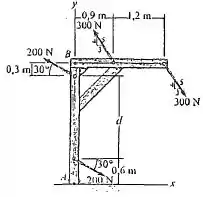
Passo 1
Então o que o enunciado quer é que dada que produz um momento binário junto com o momento binário de , qual o valor de para que o momento resultante seja igual a .
Como o momento binário é um vetor livre (causa o mesmo efeito rotacional em qualquer ponto), vamos determinar ele em relação ao ponto .
Com essa escolha podemos desconsiderar a componente vertical de de cima e da força de de baixo e podemos desconsiderar também as componentes horizontais das forças , que têm suas linhas de ação passando por , já que elas não irão influenciar no momento.
Vamos calcular o momento binário usando a análise escalar:
Onde é a intensidade das forças e é a distância perpendicular ou braço de momento entre as forças.
Nessa situação teremos que decompor nossas forças na vertical e na horizontal, para isso vamos usar o que a figura nos dá, que é aquele pequeno triangulo nos vetores das forças que indica uma proporcionalidade, então se quisermos a componente vertical da força , basta multiplicá-la por e se quisermos a horizontal, multiplicámos por .
O momento binário resultante é a soma dos momentos binários das forças.
Vamos adotar o sentido horário como positivo.
Passo 2
Calculando: