Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 11.Problemas - Ex. 48
Um bloco homogêneo repousa no topo da superfície cilíndrica. Derive a relação entre o raio do cilindro, r, e a dimensão do bloco b, para o equilíbrio estável. Dica: estabeleça a função energia potencial para um ângulo pequeno , ou seja,
Passo 1
Do diagrama corpo livre (DLC):
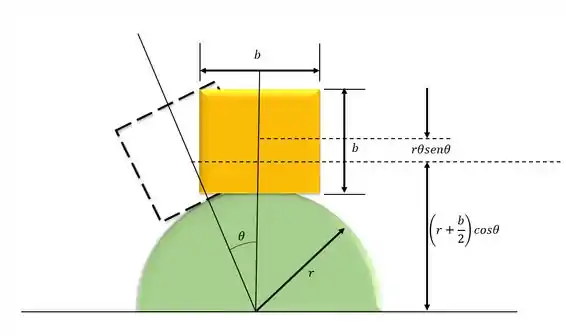
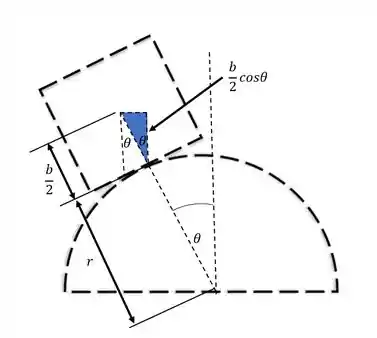
Passo 2
Da geometria da figura temos:
Passo 3
Vamos calcular a energia potencial do sistema:
Em que W é o peso do bloco. Seguindo a dica do enunciado para ângulos pequenos:
Passo 4
Com a expressão da energia potencial, podemos calcular a primeira derivada para encontrar a posição do equilíbrio:
Portanto o ângulo proporciona o equilíbrio.
Passo 5
Para analisar o equilíbrio, precisamos tomar a segunda derivada:
Portanto a relação entre b e r que confere equilíbrio estável para o sistema em 0º é
Resposta
Exercícios de Livros Relacionados
Saendo que a engrenagem da barra AB pesa 36N e a da barra CD pesa 18N, determine as posições de equilíbrio do sistema e determine em cada caso a estabilidade do equilíbrio:
Resolva o problema 10.99 se k = 3,6 k N / m , r = 75 m m ,l = 150 m m , e (a) W = 68 N eb W = 272 N .
Sabendo que as molas estão indeformadas quando y = 0 , determine o valor de y para equilíbrio quando W = 80 N ,l = 500 m m e k = 600 N / m m .
Sabendo que as engrenagens têm a mesma massa m , determine as posições de equilíbrio do sistema e determine em cada caso a estabilidade do equilíbrio:
Sabendo que as barras possuem o mesmo comprimento l e o peso da engrenagem em AB é de 13,5N e o da engrenagem da barra CD é 9N, determine as posições de equilíbrio do sistema e determine em cada caso