Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 106
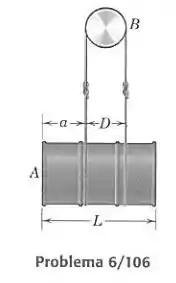
O tambor uniforme com centro de massa na metade de seu comprimento, é suspenso por uma corda que passa sobre a superfície cilíndrica fixa . O coeficiente de atrito estático entre a corda e a superfície sobre a qual ela passa é . Determine o valor máximo que a dimensão pode ter antes que o tambor tombe, saído da posição horizontal.
Passo 1
No limite de tombamento do tambor, o sistema ainda está em equilíbrio, e o coeficiente de atrito entre a corda e a superfície é . A fórmula para o equilíbrio de uma corda enrolada em torno de uma superfície é a seguinte:
Sendo e as trações maior e menor nas extremidades da fita e o ângulo total de contato da fita com a superfície, nesse caso igual a , o ângulo de meia volta. Através dessa equação acharemos uma relação entre e , e então aplicamos as equações de equilíbrio do tambor para determinar a dimensão de .
Passo 2
Vamos então aplicar a fórmula:
Passando para a forma exponencial:
Passo 3
Vamos agora representar o tambor em diagrama de corpo livre. Para que o corpo esteja em equilíbrio, o centro de massa deve estar entre as duas extremidades da corda, ou o tambor viraria para um lado. Quando é grande, a extremidade da esquerda está mais próxima do centro, e então deve ter uma tração maior, pois o braço de alavanca é menor e o momento causado deve ser igual ao da outra extremidade. Então a tração maior fica na esquerda e a tração menor fica na direita:
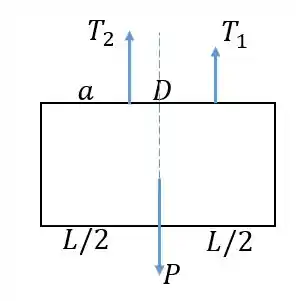
O braço de alavanca para a tração em relação ao centro é , e o braço de alavanca da tração é . Então fazemos ser zero o momento em torno do centro de massa:
Substituímos por e depois cortamos :
Resolvendo achamos o valor de em função de , e :