Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 37
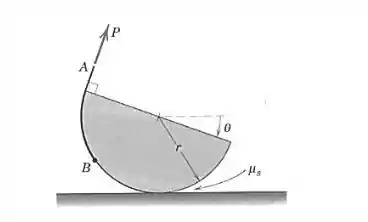
6/37) O semicilindro homogêneo repousa sobre uma superfície horizontal e estásubmetido a uma força aplicada a um cabo firmemente preso asua periferia . A força é lentamente aumentada e mantida normal à superfície plana do semicilindro . Se é observado deslizamento no instante que atinge , determine o coeficiente de atrito estático e o valor de quando ocorre o deslizamento .
Passo 1
Então galera, seja o centro da semicircunferência e o centro de massa do semicilindro , sendo assim , temos que :
Aplicando as equações de equilíbrio que conhecemos , obtemos que :
Além disso , nós sabemos que quando o deslizamento para , a força de atrito estático é dada por :
Passo 2
Bom pessoal , agora devemos fazer associações entre as equações obidas no passo anterior .
Sabemos que :
Sendo assim ,
Pela equação (2) , achamos que :
Dessa forma ,
Isolando na equação , obtemos que :
Passo 3
Combinando a equação obtida para no passo anterior com a relação (3) , achamos que :
Dessa forma , para :
Substituindo o valor de achado acima na equação de , obtemos que :
Resposta
De boa galera? Então bora resolver mais exercícios como esse!