Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 11

O poste uniforme de comprimento l e massa m está apoiado contra as superfícies mostradas. Se o coeficiente de atrito estático é μ s = 0,25 tanto em A quanto em B , determine o ângulo θ mínimo no qual o poste pode ser colocado antes que ele comece a deslizar.

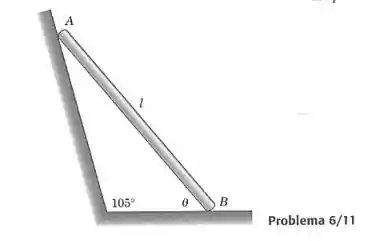
Passo 1

Vamos considerar que no caso limite a barra está na iminência de deslizar tanto em A quanto em B . Isso significa que o coeficiente de atrito é estático nos dois pontos, então o atrito é a força normal vezes μ s = 0,25 . Vamos representar as forças atuantes na barra. As forças de atrito apontam na direção que impede a barra de cair.

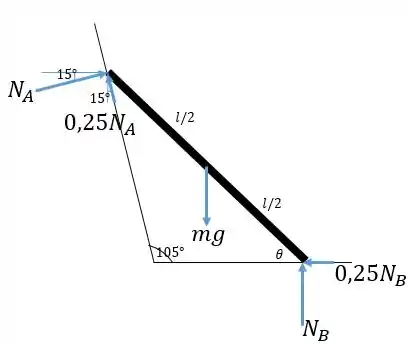
Passo 2

Temos 3 incógnitas: N A , N B e θ , então vamos resolver o sistema com 3 equações, duas de força e uma de momento. Vamos começar com o momento em torno do ponto A , nesse ponto temos forças em direções mais difíceis de serem calculadas. Então:

∑ M A = 0 ⇒ - m g l 2 cos ⁡ θ + N B l cos ⁡ θ - 0,25 N B l sen ⁡ θ = 0

Cortamos l e isolamos N B :

⇒ N B cos ⁡ θ - 0,25 sen ⁡ θ = m g cos ⁡ θ 2

⇒ N B = m g cos ⁡ θ 2 cos ⁡ θ - 0,25 sen ⁡ θ     ( 1 )

Agora vamos fazer a soma das forças horizontais:

∑ F x = 0 ⇒ N A cos ⁡ 15 ° - 0,25 N A sen ⁡ 15 ° - 0,25 N B = 0

⇒ 0,9659 N A - 0,0647 N A - 0,25 N B = 0

⇒ 0,9012 N A = 0,25 N B

⇒ N A = 0,2774 N B     ( 2 )

Por último, fazemos a soma das forças verticais:

∑ F y = 0 ⇒ N A sen ⁡ 15 ° + 0,25 N A cos ⁡ 15 ° - m g + N B = 0

⇒ 0,2588 N A + 0,2415 N A - m g + N B = 0

⇒ 0,5003 N A + N B - m g = 0       ( 3 )

Passo 3

Agora vamos resolver o sistema para encontrar θ . Primeiro, substituímos N A em função de N B encontrado em (2) na equação (3):

N A = 0,2774 N B

0,5003 N A + N B - m g = 0

⇒ 0,5003 0,2774 N B + N B - m g = 0

⇒ 0,1388 N B + N B = m g

⇒ 1,1388 N B = m g

⇒ N B = 0,8781 m g

Pegamos então esse valor de N B e substituímos na equação (1):

N B = m g cos ⁡ θ 2 cos ⁡ θ - 0,25 sen ⁡ θ

⇒ 0,8781 m g = m g cos ⁡ θ 2 cos ⁡ θ - 0,25 sen ⁡ θ

Cortamos m g e encontramos uma equação para θ :

0,8781 = cos ⁡ θ 2 cos ⁡ θ - 0,25 sen ⁡ θ

⇒ 1,756 cos ⁡ θ - 0,4391 sen ⁡ θ = cos ⁡ θ

⇒ 0,756 cos ⁡ θ = 0,4391 sen ⁡ θ

Achamos então θ através de sua tangente:

sen ⁡ θ cos ⁡ θ = tan ⁡ θ = 0,756 0,4391 = 1,72

θ = arctan ⁡ 1,72 = 59,9 °

Resposta

θ = 59,9 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6/13) Uma pessoa ( massa m 1 ) ajoelhada em um painel de compensado (massa m 2 ) deseja se empurrar e ao painel para loge da parede à direita . Determine a condição sobre μ 2 que lhe permitiria fazer
6/2) O bloco de 50k g está em repouso sobre a superfície horizontal e uma força P = 200N , cuja direção pode ser variada , é aplicada ao bloco . (a) Calcule o coeficiente de atrito estático μ s , entr
6/8) A força P é aplicada ao bloco A de 200k g , que está apoiado em cima do caixote de 100k g . O sistema está em repouso quando P é inicialmente aplicada . Determine o que acontece acada corpo se (a
6/24) Determine a faixa das massas m para o qual o bloco de 100k g está em equilíbrio . Todas as polias e roldanas têm atrito desprezível .
6/23) A figura mostra um dispositivo , chamado presilha de travamento , que prende uma corda sob tração devida às grandes forças de atrito desenvolvidas . Determine , para a posição mostrada , o coefi