Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 4
O tanque do compressor de ar está sujeito a uma pressão interna de 0,63 MPa. Se o diâmetro interno do tanque for 550 mm e a espessura da parede for 6 mm, determine as componentes da tensão que age no ponto A. Desenhe um elemento de volume do material nesse ponto e mostre os resultados no elemento.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que o nosso reservatório é cilíndrico e gera uma pressão de 0,63MPa e que tem paredes com 6mm de espessura e 275 mm de raio interno. Depois de falar isso tudo, ele nos pede o estado de tensão no ponto A. Viu?? Nem é tão difícil assim. Bora lá fazer?? Partiu??
Passo 2
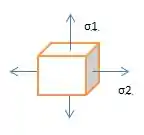
Nas questões de vasos cilíndricos de paredes finas, temos duas tensões normais: σ1 (na direção circunferencial, ou seja, do aro) e σ2 (no sentido longitudinal, ou seja, axial). No nosso caso, como o ar está confinado e comprimido dentro do tanque, ele exerce força em todos os sentidos, para tentar sair de lá, nos submetendo às duas tensões.
Disso, podemos concluir que as nossas tensões para nosso ponto A será:
Ponto A -
Passo 3
Sendo assim, temos que:
