Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas de Revisão - Ex. 166

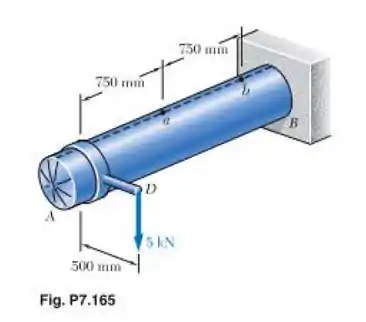
Para o tanque de ar comprimido e o carregamento do Prob. 7.165, determine a tensão normal máxima e a tensão de cisalhamento máxima no plano no ponto b no topo do tanque.

Passo 1

Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos precisar calcular a tensão interna causada pela pressão manométrica do tanque e somar com os esforços gerados pela força de 5 kN, que irá causar momento e torção no tanque. Para as pressões internas, temos que a pressão na direção longitudinal é dada por:

σ l = p r 2 t

E a pressão gerada na direção circunferencial é dada por:

σ c = p r t

Em que p é a pressão manométrica, r é o raio interno do tanque e t é a espessura da sua parede. Com esses valores, basta encontrar a tensão normal gerada pelo momento causado no eixo e a tensão de cisalhamento causada pela torção, fazendo isso teremos os valores para as tensões nas direções x, y e a tensão de cisalhamento, com isso poderemos calcular a tensão máxima através de:

σ m a x = σ m e d + R

Então vamos precisar calcular a tensão média e o raio do círculo de Mohr para o estado resultante. Bora lá!

Passo 2

Beleza! Vamos começar calculando as tensões geradas pela pressão manométrica, começando pela pressão longitudinal, temos:

σ l = p r 2 t = 1,2.10 6 0,225 0,006 → σ l = 45   M P a

Agora, na direção circunferencial, teremos:

σ c = p r t = 1,2.10 6 0,225 0,006 → 22,5   M P a

Passo 3

Beleza! Agora precisamos encontrar a tensão normal gerada pelo momento causado no tanque. Sabemos que essa tensão normal é dada por:

σ = M c I

Em que M é o momento aplicado, c é a distância do centro do tanque até o ponto de interesse e I é o seu momento de inércia. No nosso caso c será a distância do centro do tanque até a superfície, ou seja, o raio externo do tanque, que será:

c = r 2 = r 1 + t = 0,225 + 0,006 → c = 0,231   m

Já o momento M será causado pela força de 5 kN aplicada no sistema, através do braço de alavanca até o ponto b, que estamos analisando. Então o momento gerado será:

M = 5.10 3 1 , 5 → M = 750 0   N . m

E, por fim, precisamos calcular o momento de inércia da seção, como temos uma seção circular vazada, o momento de inércia será dado por:

I = π 4 r 2 4 - r 1 4

Substituindo os valores conhecidos, chegamos em:

I = π 4 0,231 4 - 0,225 4 → I = 223,45.10 - 6   m 4

Agora temos todos os valores para calcular a tensão normal causada pelo momento gerado no tanque. Então teremos:

σ = M c I = 750 0 0,231 223,45.10 - 6 → σ = 7,75   M P a

Passo 4

Agora nós vamos encontrar a tensão de cisalhamento gerada pela torção aplicada ao tanque, sabendo que o cisalhamento é dado por:

τ = T c J

Em que T é o torque aplicado ao eixo, c é a distância do centro ao ponto de interesse e J é o momento polar de inércia. No nosso caso, o torque gerado será proveniente da força de 5kN aplicada na alavanca, vezes o braço de 500 mm, ou seja:

T = 5000 0,5 → T = 2500   N . m

O c será o mesmo do passo 2, ou seja:

c = 0,231   m

E, o momento polar de inércia para uma seção circular vazada é dado por:

J = π 2 0,231 4 - 0,225 4 → I = 446,9.10 - 6   m 4

Então agora podemos calcular o valor da tensão de cisalhamento gerada pela torção, então teremos:

τ = 2500 0,231 446,9.10 - 6 → τ = 1,29   M P a

Passo 5

Então, com isso, as tensões resultantes no tanque no ponto b serão:

σ x = σ c + σ

σ y = σ l

τ x y = τ

Substituindo as expressões encontradas nos passos 2 e 3, chegamos em:

σ x = 22,5 + 7,75 → σ x = 30,25   M P a

σ y = 45   M P a

τ x y = 1,29   M P a

Com esses valores, podemos encontrar a tensão média, que é dada por:

σ m e d = σ x + σ y 2 = 30,25 + 45 2 → σ m e d = 37,6   M P a

E, agora, o raio do círculo de Mohr, que é dado por:

R = σ x - σ y 2 2 + τ x y 2 = 30,25 - 45 2 2 + 1,29 2

R = 7,49   M P a

Então a tensão normal máxima será:

σ m a x = σ m e d + R = 37,6 + 7,49 → σ m a x = 45,1   M P a

E, nós sabemos que a tensão de cisalhamento máxima no plano é o próprio raio do círculo de Mohr, então teremos:

τ m a x = R → τ m a x = 7,49   M P a

Belezaaa!! Terminamos mais um, valeeeu!

Resposta

σ m a x = 45,1   M P a

τ m a x = 7,49   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A parte cilíndrica do tanque de ar comprimido mostrado na figura é fabricada com uma placa de 8m m de espessura soldada ao longo de uma hélice formando um ângulo β = 30 ° com a horizontal. Sabendo que
Um vaso de pressão com diâmetro interno de 254m m , espessura de 6,35 m m e comprimento de 1219m m é soldado em espiral e possui duas tampas laterais rígidas. A pressão manométrica dentro do vaso é de
Para o tanque do problema 7,117 , determine a maior pressão manométrica admissível, sabendo que a tensão normal perpendicular à solda é 18k s i e a tensão de cisalhamento admissível paralela à solda é
Para o problema 7.117 , determine o intervalo de valores de β que podem ser utilizados considerando que a tensão de cisalhamento paralela à solda não deve ultrapassar 1350 psi quando a pressão manomét
Um torque de intensidade T = 12k Nm é aplicado à extremidade de um tanque que contém ar comprimido sob uma pressão de 8M P a . Sabendo que o tanque tem um diâmetro interno de 180m m e uma espessura de