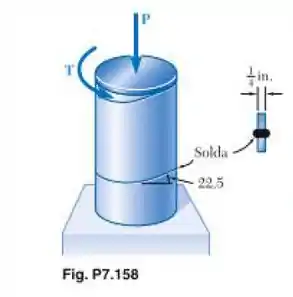
Um tubo de aço com diâmetro externo de 12 in. é fabricado a partir de uma chapa de espessura igual a 1/4 in. soldada ao longo de uma hélice que forma com o plano perpendicular ao eixo do tubo um ângulo de 22,5°. Sabendo que uma força axial P de 40 kip e um torque T de 80 kip.in., direcionados cada um como mostrado, são aplicados ao tubo, determine as tensões de cisalhamento normal e no plano, respectivamente, normal e tangencial à solda.

Beleza! Vamos começar escrevendo as equações para a tensão normal e para a tensão de cisalhamento gerada por torção, então temos:

Em que A é a área da seção transversal, c é a distância do centro até a superfície e J é o momento polar de inércia. Então vamos começar encontrando o raio interno do tubo, que será dado por:

Com isso, podemos agora calcular a área da seção transversal, onde teremos:

Agora vamos calcular o momento polar de inércia, para uma seção circular vazada, ele é dado por:

Então agora podemos calcular as tensões para o elemento sem rotação, que serão então:

Então, pela orientação das forças aplicadas ao sistema, podemos ver que não teremos tensão na direção x, então nossas tensões serão:

Agora, para encontrar as tensões normal e de cisalhamento normal e tangencial a solda, precisamos rotacionar o elemento diferencial em questão de 22,5°. Para isso, iremos contar com a ajuda das equações de transformação de tensão para uma rotação , dadas por:

Então, no nosso caso, com , ou seja, , e substituindo os valores de tensão encontrados no passo 2, teremos:

Shooow! Terminamos mais um, valeeu!