Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 104

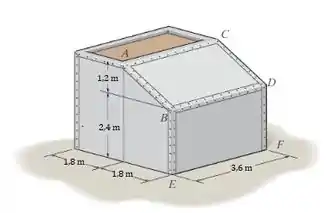
O tanque é usado para armazenar um líquido de peso específcio de 13   k N / m ³ . Se enchermos até o topo, determine a intensidade da força que o líquido exerce sobre cada um de seus dois lados A B D C e B D F E .

Passo 1

Um cara chamado Pascal enunciou uma vez que, um fluido em repouso cria uma pressão p em uma ponto que é a mesma em todas as direções. A intensidade de p , medida como uma força por área unitária, depende do peso específico γ ou densidade de massa ρ do fluido e da profundidade z do ponto a partir da superfície do fluido. Podemos escrever a expressão da pressão como:

p = γ z = t g z

Para início de questão, vamos calcular umas dimensões que estão em falta. Na face A B D C , vamos descobrir o valor de A B .

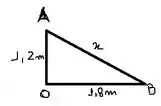
Usando o teorema de Pitágoras, temos:

x 2 = 1,2 2 + 1,8 2

x 2 = 4,68

x = 2,16   m

Passo 2

Agora precisamos encontrar o valor da pressão que o fluido causa nos pontos B e E . Para isso, podemos usar a seguinte equação:

p B = γ z = 13 1,2 = 15,6   k N / m ²

p E = γ z = 13 3,6 = 46,8   k N / m ²

A intensidade de carga nos pontos B e E pode ser calculada por:

w B = p B b = 15,6 3,6 = 56,16   k N / m

w E = p E b = 46,8 3,6 = 168,48   k N / m

Passo 3

Queremos saber as forças resultantes nas faces A B D C e B D F E pelo líquido. Vamos olhar o desenho da situação:

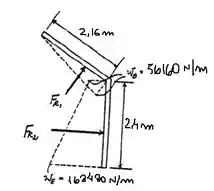
A força que atua na face A B D C é igual a:

F R 1 = 1 2 56160 2,16 = 60,6   k N

A força que atua na face B D F E é igual a:

F R 2 = 1 2 56160 + 168480 2,5 = 280,8   k N

Resposta

A intensidade da força que o líquido exerce sobre cada um dos lados é:

F R 1 = 60,6   k N

F R 2 = 280,8   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma comporta A B de 0,5 m × 0,8 m é localizada no fundo do mar de um tanque cheio de água. A comporta é articulada ao longo da aresta superior em A e repousa sem atrito em um batente em B . Determine
Um tambor de 200l i t r o s com diâmetro de 580m m é colocado de lado para atuar como uma barragem em um canal de água doce com 750m m de largura. Sabendo que o tambor é ancorado nos lados do canal, d
Resolva o problema 5.91, se a comporta pesa 4450N .
A lateral A B de um tanque aberto mede 3 m× 4 m , está articulada no fundo em A e é mantida no lugar por meio de uma haste fina B C . A força máxima de tração que a haste pode suportar sem quebrar é d
Uma calha longa é suportada por uma dobradiça contínua ao longo da aresta inferior e por uma série de cabo horizontais fixados na aresta superior. Determine a tensão em cada um dos cabos no momento qu