Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 82
A lateral de um tanque aberto mede , está articulada no fundo em e é mantida no lugar por meio de uma haste fina . A força máxima de tração que a haste pode suportar sem quebrar é de , e as especificações do projeto exigem que a força na haste não exceda desse valor. Se o tanque for cheio lentamente com água, determine a máxima profundidade admissível no tanque.
Passo 1
Bom galera, a gente vai começar fazendo um diagraminha de corpo livre, pra nortear a gente:
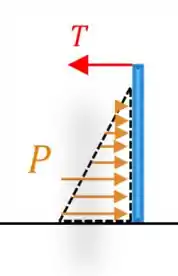
Passo 2
Vamos lá, a força de pressão que é exercida pela água é dada por:
Passo 3
Bom, mas agora, vamos analisar momento, adotando como eixo de rotação e sabendo que o corpo encontra-se em equilíbrio:
Resposta
Exercícios de Livros Relacionados
154. Substitua o carregamento distribuído por uma força resultante equivalente e especifique sua posição na viga, medindo a parti do ponto A .
150. A viga está sujeita ao carregamento distribuído. Determine o comprimento b do carregamento uniforme e sua posição a sobre a viga de modo que a força e o momento de binário resultantes que agem na
152. O vento soprou a areia sobre uma plataforma de modo que a intensidade da carga pode ser aproximada pela função w = 0,5 x 3N / m . Simplifique esse carregamento distribuído para uma força resultan
153. O concreto molhado exerce uma distribuição de pressão ao longo das paredes da forma. Determine a força resultante dessa distribuição e especifique a altura h onde o suporte deve ser colocado de m
155. Substitua o carregamento por uma força resultante e momento de binário equivalentes no ponto A .