Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 2
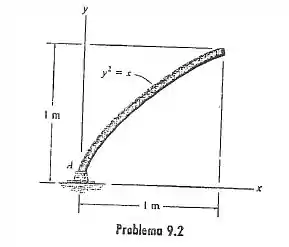
A barra uniforme é encurvada na forma de uma parábola e tem um peso por unidade de comprimento de . Determine as reações no apoio fixo .
Passo 1
Fal ai galerinha bonita, tudo beleza?
Saca só, o enunciado nos deu barra em forma da função está presa a um apoio fixo, e sabendo que seu peso por unidade de comprimento é , o enunciado quer saber quais serão as forças de reação no apoio.
Belezoca, então a primeira coisa que a gente deve fazer, é esboçar um diagrama de corpo livre pra barra, mais ou menos assim:
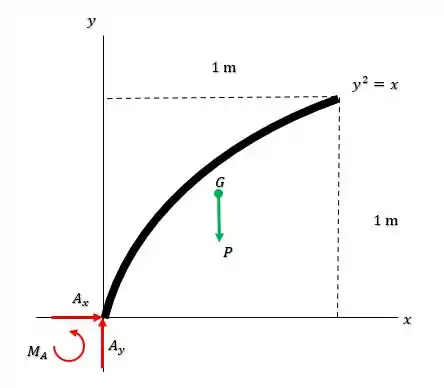
Onde o peso da barra, atua em um centro de gravidade que a gente ainda não conhece! E , são as forças reativas e o momento no ponto que precisamos encontrar.
Passo 2
Show de bolinhas, então antes de mais nada, vamos encontrar o comprimento da barra, pra gente encontrar a força de gravidade que está atuando. Então pra encontrar o comprimento da nossa barra, podemos lembrar que ela se trata de uma “linha”, ou seja, podemos usar os métodos de integração para descobrir o comprimento dessa linha, através da relação:
Logo:
Ou também podemos escrever em função de :
Onde é a função que descreve o arco. Belezinha, então se a gente tem que:
Podemos dizer que , onde é dada como . Desse modo podemos usar a segunda relação para calcular , tal que:
Sendo assim, como vai de a , teremos:
Portanto:
E como temos um peso por unidade de comprimento dado por , então o peso total da barra vai ser:
Passo 3
Belezoca, agora se a gente calcular o somatório das forças em , vamos obter que:
Logo a componente horizontal no apoio será:
Iradoso, agora fazendo o somatório no eixo , vamos obter que:
Segue que:
Passo 4
Maravilha, agora já descobrimos os valores das forças reativas no apoio em , falta a gente encontrar o momento que ele exercer devido a força pessoa atuando no sistema:
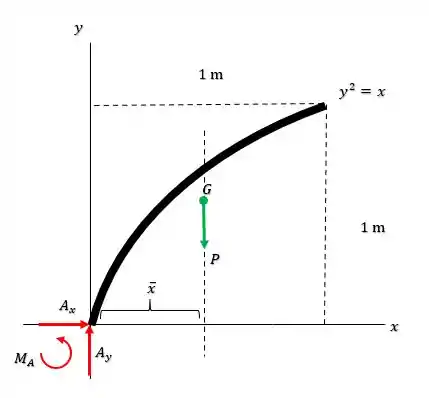
Vamos ter que:
Onde é componente do centroide onde a força atua. Ele será dado como:
Só que vimos que é o comprimento total que já encontramos, agora devemos encontrar apenas , logo:
Como , e vimos que , vamos ter que:
Só que a malandragem agora, é que sabemos que , de modo que:
Sendo assim:
Passo 5
Sendo assim, podemos calcular o somatório dos momentos de modo que:
Logo: