Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 87

A base da barragem de um lago é projetada para resistir a até 120 % da força horizontal da água. Após a construção verificou-se a disposição de lodo (que é equivalente a um líquido de densidade ρ s = 1,76 ⋅ 10 3   N / m 3 ) no fundo do lago a uma taxa de 12   m m / a n o . Considerando uma seção da barragem de 1   m de largura, determine quantos anos se passarão até a barragem deixar de ser segura.

Passo 1

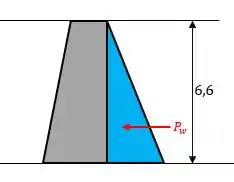
Bom galera, a gente vai começar fazendo um diagraminha de corpo livre da barragem sem o lodo, pra nortear a gente:

Passo 2

Vamos lá, a gente pode calcular a força de pressão exercida pela água horizontalmente na barragem, bem assim:

P W = 1 2 A ρ W = 1 2 A ρ g h

→ P W = 1 2 6,6 1 10 3 9,81 6,6

→ P W = 213,66   k N

Algo muito importante, é que o problema disse que a barragem estará segura até uma pressão de 120 % desse valor, então:

P m á x = 1,2 ⋅ 213,66 = 256 , 39   k N

Passo 3

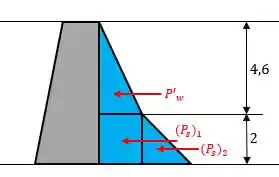
Bom, agora, vamos analisar a situação com o lodo, vamos logo fazer um diagrama de corpo livre rapidinho:

Passo 4

Agora, vamos calcular as forças de pressão exercidas pelos fluidos:

P = 1 2 A ρ g h

Calculando:

P W ' = 1 2 6 , 6 - d 1 10 3 9,81 6 , 6 - d = 4,905 6,6 - d 2   k N

P S 1 = 1 2 d 1 10 3 9,81 6,6 - d = 9,81 ( 6,6 d - d 2 )   k N

P S 2 = 1 2 d 1 1,76 ⋅ 10 3 9,81 d = 8,6328 d 2   k N

Então, a soma dessa pressões fica:

P ' = 4,905 6,6 - d 2 + 9,81 ( 6,6 d - d 2 ) + 8,6328 d 2

→ P ' = 3,7278 d 2 + 213,66   k N

Passo 5

Por fim, a gente calcula a altura de lodo acumulada d para que a P ' = P m á x , bora lá:

P ' = P m á x = 256,39 = 3,7278 d 2 + 213,66

Resolvendo a equação, a gente encontra:

d = 3,3856   m

E o tempo para o lodo acumular até essa altura é:

t = 3,3856 ⋅ 10 3 10 = 282   A n o s

Resposta

t = 282   A n o s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A comporta quadrada AB é mantida na posição mostrada na figura por meio de articulações ao longo de sua aresta superior A e por um pino de cisalhamento em B. Para uma profundidade de água d = 1m , det
Uma viga é submetida a uma carga distribuída linearmente em ordem decrescente e repousa em dois suportes largos B C e D E , que exercem cargas uniformemente distribuídas para cima como mostrado na fig
117- Quatro vigas, cada qual de comprimento 3 a , são pregadas juntas com um único prego em A , B , C e D . Cada viga é fixada a um suporte localizado a uma distância a a partir da ponta da viga como
118- Quatro vigas, cada qual de comprimento 2 a , são pregadas juntas em seus pontos médios para formar o sistema de suporte mostrado na figura. Considere que apenas forças verticais são exercidas nas
Determine as reações de apoio da viga para a carga dela.