Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 103
Determine a força única equivalente e a distância do ponto A até sua linha de ação para a viga e a carga do Problema 3.101b, Problema 3.101d, Problema 3.101e.
Passo 1
Para a letra temos o seguinte DCL:
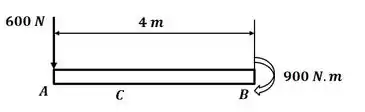
Aplicando o somatório de forças na direção temos:
E o sistema equivalente que queremos obter:
E, aplicando o somatório de momento com relação ao ponto C:
Passo 2
Para a letra temos o seguinte DCL:
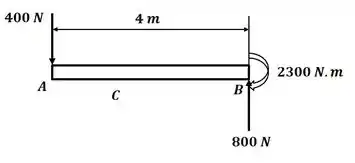
Aplicando o somatório de forças na direção temos:
E o sistema equivalente que queremos obter:
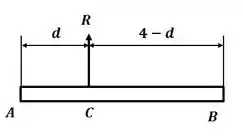
E, aplicando o somatório de momento com relação ao ponto C:
Passo 3
Para a letra temos o seguinte DCL:
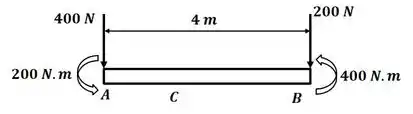
Aplicando o somatório de forças na direção temos:
E o sistema equivalente que queremos obter:
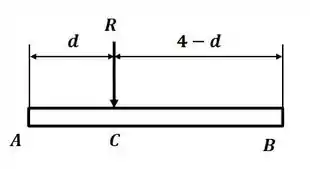
E, aplicando o somatório de momento com relação ao ponto C:
Resposta
Exercícios de Livros Relacionados
Determine (a) a distância a tal que as reações verticais dos apoios A e B sejam iguais, (b) as reações de apoio correspondentes.
Para a viga e o carregamento mostrados nas figuras, determine (a) a intensidade e a localização da resultante da carga distribuida, (b) as reações de apoio da viga.
Determine as reações de apoio da viga para o carregamento dado quando ω 0 = 2190N / m .
Determine as reações de apoio da viga para a carga dela.
Para a viga e o carregamento mostrados nas figuras, determine (a) a intensidade e a localização da resultante da carga distribuida, (b) as reações de apoio da viga.