Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 55
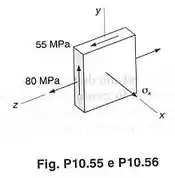
O estado de tensões mostrado ocorre em um componente de máquina, que é feito de um aço para o qual . Usando o critério da máxima energia de distorção, determinar o coeficiente de segurança em relação à tensão de escoamento, quando:
- ;
- .
Passo 1
Fala aí, pessoas lindas! Tudo certo? Espero que sim! Sem enrolação, vamos logo para o que interessa: entender o que o enunciado pediu e saber como resolver a questão!
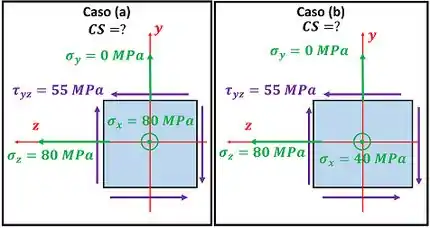
O enunciado nos mostra uma figura com um estado de tensões e pede para a gente determinar o coeficiente de segurança desse estado de tensões, usando o critério da máxima energia de distorção. Ele quer que a gente determine , usando esse critério para duas ocasiões mostradas na figura abaixo.
O critério da máxima energia de distorção usa as tensões principais , e .
O cálculo do coeficiente de segurança através desse critério é realizado, reorganizando a equação 10.36 do livro.
onde é a tensão de resistência ao escoamento do aço dada pelo enunciado .
Ou seja, para calcular , precisamos achar , e . Então vamos calcular essas tensões principais para o caso (a) no próximo passo!
Passo 2
Para calcular as tensões principais , e do caso (a), usaremos as equações de tensões principais abaixo, substituindo , , e da figura do caso (a).
Agora estamos prontos para saber o valor de do caso (a), substituindo as tensões principais na equação do critério de máxima energia de distorção.
Passo 3
Vamos substituir , e na equação do critério de máxima energia de distorção e descobrir o valor de do caso (a). Dessa forma, vamos resolver a letra (a) da questão!
Boaaaa! Encerramos a letra (a)!
Passo 4
Já que resolvemos a letra (a), vamos partir pra letra (b)
Para calcular as tensões principais , e do caso (b), usaremos as equações de tensões principais abaixo, substituindo , , e da figura do caso (b).
Agora estamos prontos para saber o valor de do caso (b), substituindo as tensões principais na equação do critério de máxima energia de distorção.
Passo 5
Vamos substituir , e na equação do critério de máxima energia de distorção e descobrir o valor de do caso (b). Desse jeito, vamos resolver a letra (b) da questão!
Shooooow! Acabamos com a letra (b) da questão e entregamos tudo o que o enunciado queria!