Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 98
A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
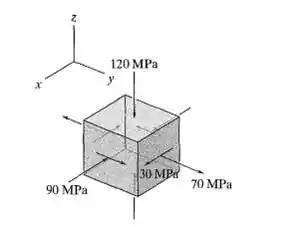
Passo 1
Fala aí pessoal. Vamos para mais uma resolução massa de problemas de resmat. Essa questão é bem simples e direta. Primeiramente, devemos determinar as tensões principais no plano, para isso, usamos a seguinte fórmula:
Substituindo na fórmula, teremos:
Portanto, podemos obter:
Além disso, podemos obter a tensão cisalhante máxima absoluta:
Resposta
Exercícios de Livros Relacionados
Uma viga de aço laminado W 250×58 suporta uma carga P conforme mostra a figura. Sabendo que P =100k N , a = 508m meσ a d m = 124,1M P a determine (a) o valor máximo da tensão normal σ m na viga,(b) o
Uma viga de aço laminado W 250×58 suporta uma carga P conforme mostra a figura.Sabendo que P =200k N , a = 254m meσ a d m = 124,1M P a determine (a) o valor máximo da tensão normal σ m na viga,(b) o v
Uma viga biapoiada com um balanço de aço laminado com um balanço de aço laminado W 920×449 suporta uma carga P conforme mostra a figura. Sabendo que P = 700k N , a = 2,5meeσ a d m = 100M P a , determi
Uma viga biapoiada com um balanço de aço laminado com um balanço de aço laminado W 920×449 suporta uma carga P conforme mostra a figura. Sabendo que P = 850k N , a = 2,0meeσ a d m = 100M P a , determi
Os problemas a seguir, se referem a um perfil de aço laminado selecionado em um problema do capítulo 5, para suportar determinado carregamento a um custo mínimo e ao mesmo tempo satisfazendo a condiçã