Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 10
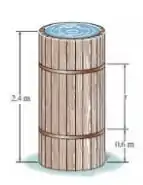
O barril está cheio de água até em cima. Determine a distância s entre o aro superior e o aro inferior de modo que a força de tração em cada aro seja a mesma. Determine também a força em cada aro. O barril tem diâmetro interno de 1,2 m. Despreze a espessura da parede. Considere que somente os aros resistam à pressão da água.
- Observação: A água desenvolve pressão no barril de acordo com a lei de Pascal, p = (900z) Pa, onde z é a profundidade da água em relação à superfície, medida em metros.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que o nosso barril tem dois aros distando de s e fazendo a mesma força de tração, sendo que o barril tem 0,6 m de raio interno. Depois de falar isso tudo, ele nos pede a distância s e a força de cada aro. Viu?? Nem é tão difícil assim. Bora lá fazer?? Partiu??
Passo 2
Nosso primeiro passo será determinar qual a força exercida pela água.
Passo 3
Com isso, podemos fazer que a soma das forças internas e dos momentos será zero, achando, assim, a força em cada aro e a distância s.