Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 104
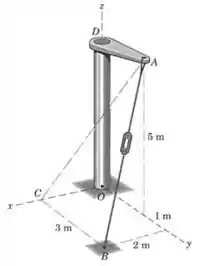
O tensionador é apertado até que a força trativa no cabo valha . Determine a expressão vetorial para a força trativa , como uma força atuando no elemento . Ache também o módulo da projeção de ao longo da linha .
Passo 1
Para encontrar a expressão vetorial para a força , primeiro precisamos encontrar um vetor unitário na direção . Para visualizar melhor o problema, vamos começar fazendo o diagrama de corpo livre.
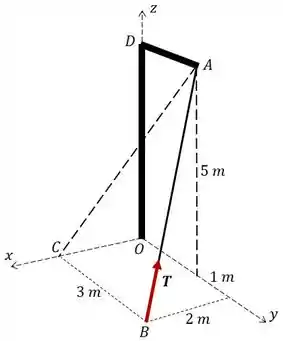
Uma dica galerinhaaa, para achar os valores cuidem onde o eixo é “espelhado” (lado oposto), exemplo para o ponto B: o eixo X espelha em um comprimento de 2m (notem que está do lado oposto) e sim para outras coordenadas deste ponto e do ponto A.
Então teremos....
Agora considerando que:
X= , y= e Z=k , se tratando de um vetor AB temos que reduzir um do outro para obter o vetor resultante AB, olhem, venham comigo, me deem a mão!!!
E agora para encontrar o vetor unitário é só dividir pelo próprio módulo:
Passo 2
E como a força tem módulo (fornecida e aponta na direção de :
Passo 3
Agora queremos projetar na linha , mas para isso precisamos escrever um vetor nessa direção. Vamos fazer algo muito parecido com o que fizemos para a direção :
Pleaseeeee não esqueçam olhem os valores projetados, como mencionado no passo 1
E encontramos o vetor unitário :
E para encontrar a projeção de em é só fazer o seguinte produto escalar:
E vamos chamar essa projeção de :
Ufaaaaaaaaaaaa vencemos 0/