Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas Fundamentais - Ex. 15
Expresse a força como um vetor cartesiano.
Passo 1
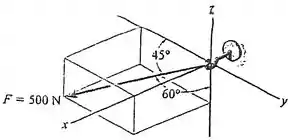
Cara, vamos entender o que ele quer e o que essa figura nos quer dizer. Ele quer que a gente expresse essa força como vetor, aí precisamos achar as componentes dessa força nos eixos coordenados.
Mas e essa figura estranha? Cara, ele tá dizendo que temos uma força de módulo . Ela faz um ângulo de em relação a parte negativa do eixo . E faz com a parte negativa de .
Ele não específica o ângulo que a força faz com , mas a gente consegue descobrir, fica tranquilo.
Aí a parada é usar nossos ângulos dados para achar as componentes os eixos coordenados.
Bora lá!
Passo 2
Para encontrar as componentes da força nos eixos, podemos usar os ângulos diretores e as fórmulinhas:
Vamos olhar cada uma dessas. A que nos dá a componente de é:
Esse ângulo está entre a força e a parte positiva de . Mas lembra que ele deu o ângulo entre a força e a parte negativa de como ? Temos algo assim:
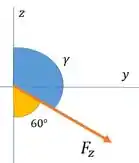
Podemos achar fazendo
Jogando na fórmulinha:
Temos a mesma situação para o eixo . é o ângulo entre força e a parte negativa de . Aí a gente faz
Passo 3
Já para o eixo não temos o ângulo, mas podemos tirar pela fórmulinha:
Logo, nossa componente em :
Passo 4
Por fim, escrevendo nossa força como vetor cartesiano:
Repare que a direção e é negativa pois a componente e apontam para trás e para baixo.