Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 90
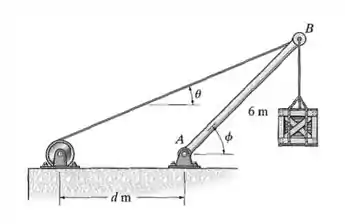
A lança é suportada pelo cabo do guincho com diâmetro de com tensão normal admissível . Determine a maior carga que pode ser suportada sem provocar a ruptura do cabo quando e . Despreze o tamanho do guincho.
Passo 1
E aí meus consagrados, como vocês estão? Prontos pra mais uma questão?
Pois então bora, o que nós desejamos com essa questão é determinar maior carga que pode ser suportada sem provocar a ruptura do cabo, sendo assim, vamos definir aqui todas as nossas constantes de acordo com a notação que usaremos nesse problema da seguinte forma
Além disso vamos nós temos que a tração no cabo pode ser descrita como sendo
Porque a tensão é força sobre área correto?
Passo 2
A partir da relação entre a tração no cabo, a área e a tensão vamos ter:
Substituindo os valores:
Passo 3
Agora, sabendo que o nosso sistema está em equilíbrio isso vai implicar que o somatório das forças em uma determinada direção deve ser igual a 0. Dessa forma, aplicaremos as equações de equilíbrio ao longo dos eixos e obtendo o seguinte para o eixo
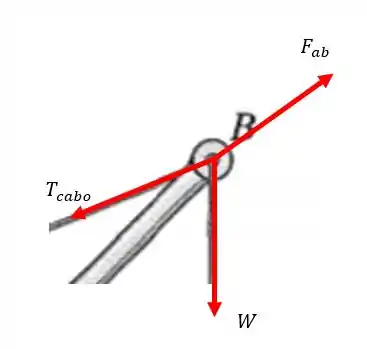
Aqui a gente teve de decompor as forças em por isso utilizamos o cosseno de ambos os ângulos e vale lembrar também que a tensão do cabo é negativo porque aponta para a esquerda.
De forma análoga faremos ao longo do eixo obtendo
Considerando como a força peso. E lembrando que agora a decomposição se dará na vertical vamos ter que utilizar o seno dos ângulos:
Pronto, tá finalizado o nosso problema.