Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 102

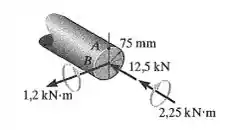
As cargas internas que agem sobre uma seção transversal no eixo de acionamento de uma turbina de 150 mm de diâmetro consistem em uma força axial de 12,5 kN, um momento fletor de 1,2 kN.m e um momento de torção de 2,25 kN.m. Determine as tensões principais no ponto B. Calcule também a tensão de cisalhamento máxima no plano nesse ponto.

Passo 1

Fala aí pessoal, tudo belezinha?

O primeiro passo desse problema é calcular as tensões no ponto B. Os esforços atuantes são:

N = 12,5 k N

T = 2,25 k N m

M = 1,2 k N m

Logo as tensões neste ponto são dadas pelas fórmulas abaixo:

σ b = - N A = - 12,5 × 10 3 π × 0,075 2

σ b = - 0,707   M P a

E para τ b :

τ b = T c J = 2,25 × 10 3 × 0,075 π 2 × 0,075 4

τ b = 3,395   M P a

Passo 2

Com as tensões no ponto calculadas, o próximo passo é calcular as tensões principais através da fórmula:

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

Substituindo os valores na fórmula acima, ficamos com:

σ 1 = 3,06 M P a

σ 2 = - 3,766 M P a

A tensão cisalhante máxima será dada pelo próprio raio do círculo de Mohr:

τ m á x = σ x - σ y 2 2 + τ x y 2

τ m á x = 3,41 M P a

Resposta

σ 1 = 3,06 M P a

σ 2 = - 3,766 M P a

τ m á x = 3,41 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um material está sujeiro às tensões principais σ x e σ y . Determine a orientação θ de um extensômetro coloca em um ponto, de modo que sua leitura da deformação normal responda apenas a σ y e não a σ
As cargas internas que agem sobre uma seção transversal no eixo de acionamento de uma turbina de 150 mm de diâmetro consistem em uma força axial de 12,5 kN, um momento fletor de 1,2 kN.m e um momento
A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
Resolva o Problema 9.96 para o ponto B.
Foi definido na Seção 8,2 que as tensões de cisalhamento produzidas em um eixo pelas cargas transversais são geralmente muito menores que aquela produzidas por torque . Nos Problema anteriores, seu ef