Um terminal marítimo para descarga de trigo a granel de um navio é equipado com um tubo vertical com um bocal em que suga o trigo para cima pelo tubo e o transfere para o edifício de armaznemaneto. Calcule as componentes e da força necessária para variar a quantidade de movimento de escoamento da massa para contornar a curva. Identifique todas as forças aplicadas externamente à curva e a massa em seu interior. O ar escoa através do tubo com de diâmetro na taxa de por hora sob um vácuo de demercúrio ( manométrica) e carrega consigo de trigo por hora a uma velocidade de .

Agora vamos analisar as forças resultantes em cada direção, usando a equação do escoamento. Começando pela direção :

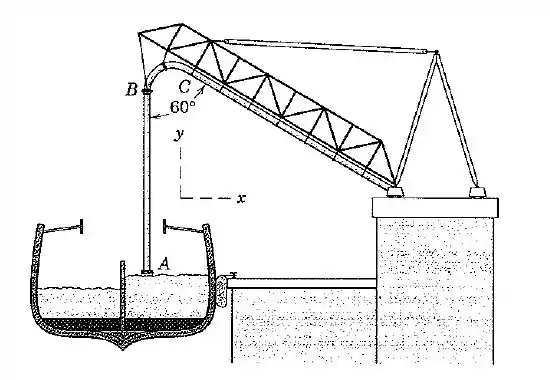
A velocidade de entrada é perpendicular a entrada do cano em (veja a figura), ou seja, é perpendicular a direção :

E a velocidade de saída forma um ângulo de com a vertical, então:

Agora é só substituir na fórmula:

E agora podemos fazer a mesma coisa para a direção vertical:

Então a força resultante necessária é:

Agora falta identificar todas as forças aplicadas externamente à porção curvada do cano e à massa que passa por ela. Não precisamos calcular essa forças, só precisamos identifica-las.

Em primeiro lugar temos a força associado à pressão manométrica gerada pelo vácuo, que foi mencionado no enunciado. Além disso temos o peso do próprio cano e o peso da massa que transita por ali, e a tensão que o cano exerce sobre a massa para mantê-la em sua trajetória.

Ok, mas e as forças que mantém o cano na sua posição? Sendo bastante específicos, precisamos dizer que existe um momento fletor na posição , já que o cano tende a se “curvar” para dentro com o peso do trigo, e existe uma tensão de cisalhamento na mesma posição, já que o guindaste “puxa” o cano para cima e o peso do trigo o “puxa para baixo”.