Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 20

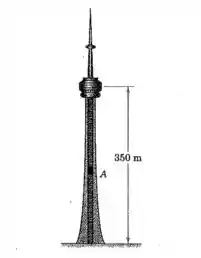
O elevador principal da torre CN em Toronto sobe cerca de e na maior parte de seu curso tem uma velocidade constante de . Suponha que tanto a aceleração quanto a desaceleração tenham módulo constante de e determine o tempo de duração do curso do elevador.

Passo 1

A primeira coisa a fazer é desobrir quanto tempo esse elevador leva para ir da velocidade até :

Sabendo que a aceleração é:

Então o tempo de aceleração é:

E sabemos que a resposta será a mesma para a desaleração:

Passo 2

Beleza, agora precisamos saber qual a distância percorrida pelo elevador enquanto ele está sendo acelerado até a velocidade máxima. Vamos usar a equação de Torricelli:

E a distância será a mesma para a desaceleração. Isso quer dizer que a distância que o elevador percorre enquanto é acelerado/freado é:

E ainda fica faltando percorrer:

Passo 3

Ok, o enunciado já diz que na maior parte desse trajeto a velocidade do elevador é , então o tempo que ele demora para percorrer é:

E agora já podemos calcular o tempo total:

Resposta

O tempo de duração do curso é .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro está se movendo a 15m / s , quando um semáforo, 50m à sua frente, acende a luz amarela. Determine a desaceleração constante exigida do carro e o tempo necessário para parar no semáforo.

Uma bola é solta da parte de baixo de um elevador que está se movendo para cima com uma velocidade de 2 m/s. Se a bola bate no fundo do poço do elevador em 3 s, determine a altura do elevador a partir

Se uma partícula tem uma velocidade inicial de v 0 = 12m / s para a direita, em s 0 = 0 , determine a sua posição quando t = 10s , se a = 2m / s 2 para a esquerda.

Um trem parte do repouso em uma estação e move-se com uma aceleração constante de 1m / s 2 . Determine a velocidade do trem quando t = 30s e a distância percorrida durante este tempo.

Um carro parte do repouso e com aceleração constante chega a uma velocidade de 15 m/s quando percorre uma distância de 200 m. Determine a aceleração do carro e o tempo exigido.