Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 83
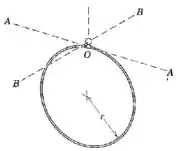
O anel circular de raio está suspenso a partir de uma cavidade (não mostrada) que se encaixa na pequena esfera de fixação em . Determine a razão entre o período para pequenas oscilações em torno do eixo - e o em torno do eixo -. Despreze o pequeno deslocamento, massa e atrito da esfera.
Passo 1
Como só queremos calcular a razão entre os dois períodos, vamos escrever uma equação genérica, que serve para qualquer um dos eixos:
E a soma dos momentos será alguma coisa constante multiplicada por , com um sinal negativo na frente para indicar que esse momento favorece o retorno à posição de equilíbrio:
Então:
E o termo que multiplica é o quadrado da frequência angular do oscilador, então:
Essa frequência pode ser reescrita em função do período:
Como essa constante será a mesma () nos caso dos dois eixos, a razão que estamos procurando é a seguinte:
Passo 2
Então agora vamos calcular os momentos de inércia em relação a cada um dos eixos. Em ambos os casos vamos usar o teorema dos eixos paralelos:
Onde (nos dois casos) é a distância entre o centro de massa e o ponto , que é comum aos eixos:
Mas o momento de inércia em relação a um eixo que cruza o centro de massa é diferente para cada caso, e pode ser consultado em uma tabela:
Então:
Ou seja:
Resposta
A razão entre os períodos é .