Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 70

Em um teste de tanque de água envolvendo o lançamento de um pequeno modelo de barco, a velocidade horizontal inicial do modelo é 6 m/s, e sua aceleração horizontal varia linearmente de -12 m/s² em t = 0 a -2 m/s²2 em t = t1 e então permanece igual a –2 m/s² até t = 1,4 s. Sabendo que v = 1,8 m/s quando t = t1, determine (a) o valor de t1, (b) a velocidade e a posição do modelo em t = 1,4 s

Passo 1

Dados: v 0 = 6 m / s ;   f o r   0 ≤ t ≤ t , a × t

Para t 1 ≤ t ≤ 1.4 s                           a = - 2 m / s 2

Em t = 0       a = - 12 m / s 2 ;         e m   t = t 1

a = - 2 m / s 2 , v = 1.8 m / s 2

Passo 2

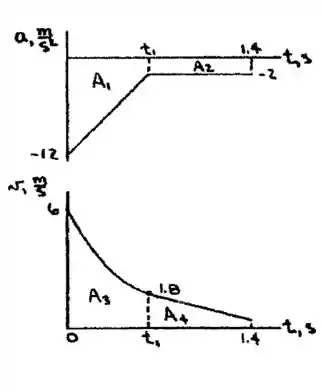
O a - t   e     v - t curvas são desenhadas primeiro como mostradas:

(a) nós temos v t 1 = v 0 + A 1

Ou 1.8 m / s = 6 m / s - t 1 s 12 + 2 2 m / s 2

Ou t 1 = 0.6 s

Passo 3

(b) Nós temos v 1,4 = v t 1 + A 2

Ou v 1.4 = 1.8 m / s - ( 1.4 - 0.6 ) 5 × 2 m / s 2

Ou v 1.4 = 0.20 m / s

Agora x 1,4 = A 3 + A 4 , em que A 3 é facilmente determinado usando Integração. Então:

p a r a   0 ≤ t ≤ t 1 : a = - 2 - ( - 12 ) 0.6 t - 12 = 50 3 t - 12

agora: d v d t = a

= 50 3 t - 12

Passo 4

E m   t = o ,   v = 6 m / s : ∫ 6 v   d v = ∫ 0 r   50 3 t - 12 d t

Ou v = 6 + 25 3 t 2 - 12 t

Nós temos: d x d t = v = 6 - 12 t + 25 3 t 2

Então: A 3 = ∫ 0 x 1 / 1   d x = ∫ 0 0.6   6 - 12 t + 25 3 t 2 d t

= 6 t - 6 t 2 + 25 9 t 3 0 0.6 = 2.04 m

Além disso: A 4 = ( 1.4 - 0.6 ) 1.8 + 0.2 2 = 0.8 m

Então: x 1.4 = ( 2.4 + 0.8 ) m

Ou x 1.4 = 2.84 m

Resposta

(a) t 1 = 0.6 s

(b) v 1.4 = 0.20 m / s

x 1.4 = 2.84 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O elevador mostrado na figura sai do repouso e se movimenta para cima com aceleração constante. Se o contrapeso W se movimenta 10 m em 5 s , determine (a) a aceleração do elevador e do cabo C, (b) a v
O bloco deslizante A move para a esquerda com a velocidade constante de 6 m / s . Determine c
O colar A parte do repouso e se movimenta para cima com aceleração constante. Sabendo que depois de 8 s a velocidade relativa do colar B em relação ao colar A é 600 m m / s , determine (a) as aceleraç
Caixas são colocadas em uma calha em intervalos uniformes de tempo t R e deslizam para baixo na calha com aceleração uniforme. Sabendo que quando uma caixa B qualquer é liberada, a caixa precedente A
Dois automóveis A e B estão se aproximando em pistas adjacentes de uma rodovia. Em t = 0 , A e B estão distanciados em 1 k m entre si, suas velocidades escalares são v A = 108 k m / hev B = 63 k m / h