Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 44

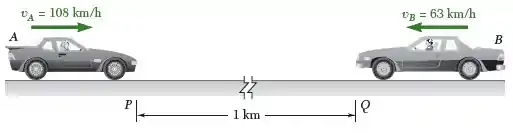
Dois automóveis A e B estão se aproximando em pistas adjacentes de uma rodovia. Em t = 0 , A e B estão distanciados em 1 k m entre si, suas velocidades escalares são v A = 108 k m / h   e   v B = 63 k m / h , e eles estão nos pontos P e Q, respectivamente. Sabendo que A passa pelo ponto Q 40 s depois que B passou por ali e que B passa pelo ponto P 42 s depois que A passou por lá, determine (a) as acelerações uniformes de A e B, (b) quando os veículos se cruzam, (c) a velocidade de B naquele instante.

Passo 1

E ai gurizada tudo certinho? O enunciado pede que a gente determine as acelerações uniformes de A e B, (b) quando os veículos se cruzam, (c) a velocidade de B naquele instante, então vamos começar trazendo as informações do enunciado partiu?

Temos x A = 0 + ( v A ) 0 t + 1 2 a A t ² ( v A ) 0 = 108 k m / h = 30 m / s

  1. Em t = 40 s : 1000 m = ( 30 m / s )   x   ( 40 s ) + 1 2 a A   x   ( 40 s ) ²

    2. x B = 0 + ( v B ) 0 t + 1 2 a B t ² ( v B ) 0 = 63 k m / h = 17,5 m / s

    Em t = 42 s : 1000 m = ( 17,5 m / s )   x   ( 42 s ) + 1 2 a B   x   ( 42 s ) ²

    a B = 0,30045 m / s ²

    Passo 2

    Agora sim podemos começar resolver as coisas, partiu?

  2. Quando os carros passam um pelo outro

    3. x A = x B = 1000 m

    Então: ( 30 m / s ) t A B + 1 2   x   ( - 0,250 m / s ) t A B 2 + ( 17,5 m / s ) t A B

    + 1 2   x   ( 0,30045 m / s ² ) t A B 2 = 1000 m

    0,05045 t A B 2 + 95 t A B 2 - 2000 = 0

    Resolvendo t = 20,822 s e t = - 1904 s

    Passo 3

  3. Temos: v B = ( v B ) 0 + a B t

Em t = t A B : v B = 17,5 m / s + ( 0,30045 m / s ² )   x   ( 20,822 s ) = 23,756 m / s

Resposta

  1. a A = - 0,250 m / s ²

    2. a B = 0,300 m / s ²

  2. t > 0 t A B = 20,8 s
  3. v B = 85,5 k m / h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula se move ao longo de uma linha reta com uma aceleração de a = 10 - 0,2 s m / s 2 , onde s é medido em metros. Determine a velocidade da partícula quando s = 10m se v = 5m / s em s = 0 .
A aceleração de uma partícula se movendo ao longo de uma linha reta é a = k / v , onde k é uma constante. Se s = 0 , v = v 0 quando t = 0 , determine a velocidade da partícula como uma função do tempo
Um carro está se movendo a 15m / s , quando um semáforo, 50m à sua frente, acende a luz amarela. Determine a desaceleração constante exigida do carro e o tempo necessário para parar no semáforo.
Uma bola é solta da parte de baixo de um elevador que está se movendo para cima com uma velocidade de 2 m/s. Se a bola bate no fundo do poço do elevador em 3 s, determine a altura do elevador a partir
Se uma partícula tem uma velocidade inicial de v 0 = 12m / s para a direita, em s 0 = 0 , determine a sua posição quando t = 10s , se a = 2m / s 2 para a esquerda.