Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 05

Os torques são exercidos nas polias A, B e C. Sabendo-se que ambos os eixos são maciços, determinar a máxima tensão de cisalhamento:

  1. No eixo AB;
  2. No eixo BC.

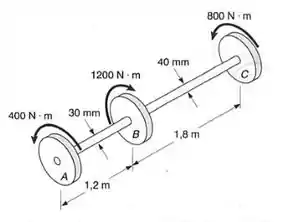
Passo 1

Nesse exercício queremos saber a máxima tensão cisalhante que age em cada trecho da barra, sendo assim teremos que a fórmula que iremos usar é a seguinte:

τ = T ρ J

Como queremos o máximo, vamos usar o raio máximo que vai ser dado por:

ρ A B = r A B = D A B 2 = 30 2 = 15   m m

ρ B C = r B C = D B C 2 = 40 2 = 20 m m

E no momento polar de inércia teremos que:

J A B = π r A B 4 2 = π 15 4 2

J B C = π r B C 4 2 = π 20 4 2

Substituindo teremos que:

τ = T r π r 4 2 = 2 T π r 3

E agora só falta os momentos fletores, que teremos:

  • Trecho AB

  • Trecho BC

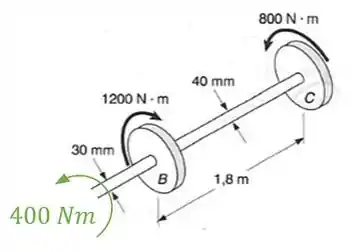
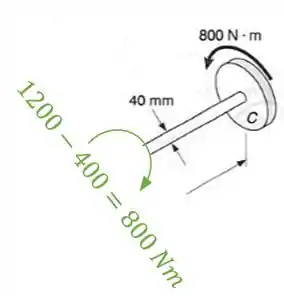
Agora basta substituirmos nas fórmulas:

τ A B = 2 T A B π r A B 3 = 2   .   400 π 15 3 = 0,07545 k N m m 2 = 75,45   M P a

τ B C = 2 T B C π r B C 3 = 2   .   800 π 20 3 = 0,06366 k N m m 2 = 63,66   M P a

Resposta

  1. τ A B = 75,45   M P a

  2. τ B C = 63,66   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para reduzir a massa total do conjunto do Problema 3.13, está sendo considerado um novo projeto no qual o diâmetro do eixo BC será menor. Determine o menor diâmetro do eixo BC para o qual o valor máxi
A tensão de cisalhamento admissível é de 103 MPa na barra de aço AB de 38,1 mm de diâmetro e 55 MPa na barra BC de 45,7 mm de diâmetro, desprezando o efeito de concentração de tensão, determine o maio
A tensão de cisalhamento admissível é de 103 MPa na barra de aço AB e 55 MPa na barra de latão BC. Sabendo que um torque τ = 1130 N ⋅ m é aplicado em A e desprezado o efeito das concentrações de tensã
A seção transversal cheia mostrada na figura é feita de latão para o qual a tensão de cisalhamento admissível é de 55 MPa. Desprezando o efeito das concentrações de tensão, determine os menores diâmet
A haste sólida AB tem um diâmetro d A B = 60m m e é feita de aço para o qual a tensão de cisalhamento admissível é de 85 MPa. O tubo CD, que tem o diÂmetro externo de 90 mm e espessura de parede de 6