Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 13
A roda de rola em seu eixo subindo a inclinação circular sob a ação do peso de preso a uma corda ao redor do aro. Determine o ângulo em que a roda para, supondo que o atrito seja suficiente para evitar o escorregamento. Qual é o coeficiente mínimo de atrito que permitirá que essa posição seja alcançada sem escorregar?
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o ângulo em que a roda para, supondo que não há escorregamento. Inicialmente a roda está em movimento sob a ação do peso de . Além disso, pede para determinar o coeficiente de atrito mínimo para que essa posição seja alcançada sem que a roda escorregue.
Então bora resolver! Vamos começar analisando o diagrama de corpo livre da estrutura.
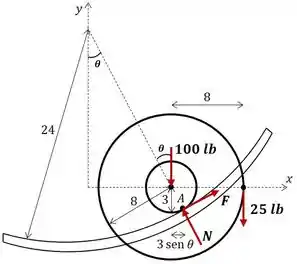
Passo 2
Com o diagrama de corpo livre fica mais fácil de visualizar né?
No instante em que a roda para ela está em equilíbrio, então podemos utilizar as equações de equilíbrio para determinar nossas incógnitas. Para determinar o ângulo , vamos fazer o equilíbrio de momentos em torno de , dessa forma dispensamos a necessidade de calcular e , que estão sendo aplicadas nesse ponto. Logo:
Passo 3
Show de bola, tranquilo de fazer né?! Sabendo esse ângulo , podemos usar o somatório de forças nas direções e para determinar e :
Passo 4
Ta, mas e agora? Como determinamos ?
Calma que agora ficou simples! Sabemos que a força de atrito máxima é dada por:
Mas nós já determinamos a força de atrito máxima e a normal pela condição de equilíbrio no item anterior, então temos que:
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 