Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 18
O bloco retangular homogêneo de massa repousa sobre o plano inclinado que é articulado em torno de um eixo horizontal através de . Se o coeficiente de atrito estático entre o bloco e o plano for , especifique as condições que determinam se o bloco inclina antes de escorregar ou escorregar antes de inclinar conforme o ângulo é gradualmente aumentado.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar as condições para que o bloco de massa apoiado no plano articulado: tombe antes de escorregar e escorregue antes de tombar. Considerando que o coeficiente de atrito entre o bloco e o plano é e que o ângulo aumenta gradualmente.
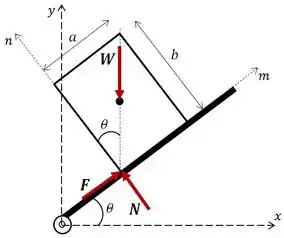
Este é um problema mais analítico do que de cálculo de fato. Então vamos começar entendendo o comportamento do bloco à medida de aumenta. Sabemos que o momento em que o bloco começa a escorregar ou tombar é quando o seu centro de gravidade se encontra à esquerda do ponto , ou seja, quando o peso do bloco faz um momento no sentido anti-horário em torno de .
Neste caso, o que vai determinar se o corpo escorrega ou tomba, é o atrito entre o bloco e a superfície. Se a força de atrito for suficiente para suportar o peso do bloco, ele tombará. Caso contrário, ele deslizará pela superfície. Show de bola! Vamos guardas essas informações por enquanto!
Passo 2
Sabemos ainda que a força de atrito máxima (necessária para suportar o peso do bloco) é dada por:
Vamos então fazer o somatório de forças na direção (indicada no diagrama de corpo livre), que deve ser nulo para que o corpo esteja em equilíbrio:
E pela equação de atrito máximo:
Passo 3
Até aqui tá dando para acompanhar né? Então bora continuar!
Pela mesma condição de equilíbrio do corpo, o somatório de forças na direção (perpendicar a no diagrama de corpo livre) também deve ser nulo. Logo:
Que é a força de atrito real atuando no sistema.
Passo 4
Como dissemos no Passo 1, para que o bloco tombe, a força de atrito real deve ser menor que a força de atrito máxima. Logo:
Temos ainda que esse mesmo ângulo pode ser obtido geometricamente por:
Igualando os resultados, temos que, para o bloco tombar:
E na condição contrária, para o bloco deslizar:
Até que não foi difícil, né? Então partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 
Resposta
Para o bloco deslizar:
Para o bloco tombar: