Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 15

A barra esbelta uniforme tem um rolo ideal em sua extremidade superior A. Se o coeficiente de atrito estático em B for μ s =   0,25 , determine o ângulo mínimo θ para o qual o equilíbrio é possível. Repita para μ s =   0,50 .

Passo 1

Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar o valor mínimo do ângulo θ para que o corpo esteja em equilíbrio em duas situações: i quando μ s =   0,25 e i i quando μ s =   0,50 .

Então bora resolver! Vamos começar analisando o diagrama de corpo livre da estrutura.

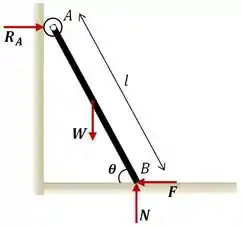
Onde l e W são, respectivamente, o comprimento e o peso da barra.

Uma vez que o corpo está em equilíbrio, podemos usar as equações de equilíbrio de forças e momentos para descobrir nossas variáveis. Fazendo o somatório de forças nas direções x e y temos:

∑ F x = 0

R A - F = 0

R A = F

∑ F y = 0

N - W = 0

N = W

Passo 2

Além disso, para a condição de equilíbrio, temos:

F ≤ μ s N

Para o primeiro caso, temos na condição limite que μ s = 0,25 :

F = 0,25 W

∴ R A = 0,25 W

Passo 3

Finalmente, fazendo o equilíbrio de momentos em torno de B :

∑ M B = 0

W * l 2 cos ⁡ θ - R A * l sen ⁡ θ = 0

W * l 2 cos ⁡ θ = 0,25 W * l sen ⁡ θ

sen ⁡ θ cos ⁡ θ = 1 2 * 0,25

tan ⁡ θ = 1 0,50

θ = tan - 1 ⁡ 1 0,50

θ = 63,4 °

Passo 4

Para o segundo caso, basta a gente substituir μ s = 0,50 na equação:

F = 0,50 W

∴ R A = 0,50 W

E pelo equilíbrio de momentos em torno de B :

∑ M B = 0

W * l 2 cos ⁡ θ - R A * l sen ⁡ θ = 0

W * l 2 cos ⁡ θ = 0,50 W * l sen ⁡ θ

sen ⁡ θ cos ⁡ θ = 1 2 * 0,50

tan ⁡ θ = 1 0,50

θ = tan - 1 ⁡ 1 1,0

θ = 45 °

Ufa! Essa já foi hein? Partiu pra próxima!

HYPERLINK "https://emojiterra.com/pt/rosto-piscando/"

Resposta

θ = 63,4 °

θ = 45 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro D de 10k g , que está preso a uma pequena polia B , é colocado na corda conforme a figura. Determine o menor ângulo θ de modo que a corda não deslize pelo pino em C . O cilindro em E tem u
Determine a menor força na alavanca P necessária para impedir que a roda gire se ela estiver sujeito a um torque de M = 250N ⋅ m . O coeficiente de atrito estático entre a correia e a roda é μ s = 0,3
Determine a força desenvolvida na mola A B a fim de evitar que a roda gira quando estiver sujeita a um momento de binário M = 200N ⋅ m . O coeficiente de atrito estático entre a correia e a borda da r
A polia de transmissão B em um gravador de fita de vídeo se encontra na iminência do deslizamente quando está sujeito a um torque M = 0,005N ⋅ m . Se o coeficiente de atrito estático entre a fita e a
Se a corda der três voltas completas mais a volta básica ( 165 ° ) em torno do pino, determine se o homem de 80k g pode evitar que a caixa de 300k g se mova. Os coeficientes de atrito estático entre a