Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 18
Um torque de intensidade é aplicado ao eixo do trem de engrenagens mostrado. Sabendo-se que os diâmetros dos três eixos maciços são, respectivamente, , e , determinar a máxima tensão de cisalhamento no: (a) eixo ; (b) eixo ; (c) eixo .
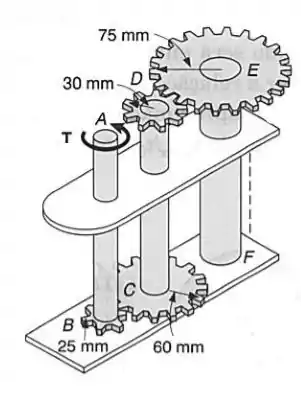
Passo 1
Aqui temos um trem de engrenagens onde o troque é transmitido desde o eixo até o eixo , como cada eixo está acoplado a engrenagens de diferentes raios teremos torques diferentes, seguindo a seguinte lógica.
Nas engrenagens a força entre elas é a mesma, logo o torque será diferente, lembrando que:
No caso das engrenages a distância será equivalente ao raio. Como temos que as forças será iguais, podemos mudar essa equação para se tornar um pouco mais prática:
Ou
Como as forças são iguais, vamos ter que
Com isso vamos ter a relação entre os torques atuantes em cada barra. Assim, basta substituir na equação do torque:
Onde:
- Representa a tensão de cisalhamento.
- A torção a qual a barra está submetida.
- A distância do centro ao ponto de aplicação.
- O momento de inércia polar.
Lembrando que o momento de inércia polar é calculado como:
Passo 2
Vamos utilizar a seguinte equação demonstrada no passo 1, para saber a relação entre os torques , e
Logo vamos ter
Como o torque de é igual a
E
Como o torque de é
Passo 3
Antes de calcularmos a tensão cisalhante de cada eixo, vamos calcular o momento de inércia polar. Lembrando que o momento de inércia polar é calculado como.
Para o eixo , que possui raio igual a :
Para o eixo , que possui raio igual a :
Para o eixo , que possui raio igual a :
Passo 4
Agora vamos utilizar a equação do torque para achar as tensões máximas de cisalhamento. Para o eixo :
Passo 5
Agora vamos utilizar a equação do torque para achar as tensões máximas de cisalhamento. Para o eixo :
Passo 6
Agora vamos utilizar a equação do torque para achar as tensões máximas de cisalhamento. Para o eixo :
Resposta
a) Para AB
b) Para CD
c) Para EF