Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 117
117- A placa retangular mostrada na figura tem peso de e é mantida na posição mostrada pelas dobradiças e e pelo cabo . Considerando que a dobradiça em não exerce qualquer esforço axial, determina a tração no cabo e as reações em e .
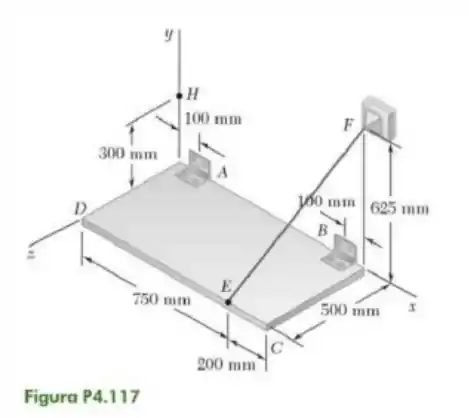
Passo 1
Como não exerce nenhuma resistência axial, logo e a força peso está no meio da placa que é:
Isso faz com que o sistema de forças na placa fique da seguinte maneira.
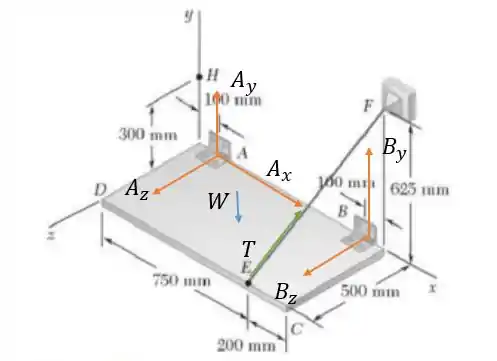
A vetorização da força ficará:
Passo 2
Agora vamos fazer a somatória dos momentos das forças em . Sabendo que as distâncias relativas das forças serão:
Dessa forma a somatória dos determinantes dos momentos em serão iguais a:
Fazendo esses determinantes temos:
Somando as componentes que tem nós temos:
Isso responde a letra a.
Agora somando as componentes que tem temos:
E as componentes que tem :
Dessa forma a reação em será:
Passo 3
Para encontrar a reação em vamos fazer a somatória das forças no sistema ser zero:
Somando as componentes que tem nós temos:
Agora as componentes que tem :
Agora as que tem :
O que nos dá uma forma vetorizada da reação em igual a: