Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 63
Se cada membro da treliça espacial pode sustentar uma força máxima de sob compressão e sob tração, determine a maior força que a treliça pode sustentar.
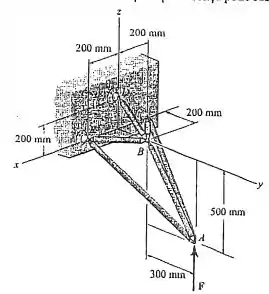
Passo 1
Para determinar a força , deve-se fazer o processo padrão para determinar as forças em cada membro aplicando o diagrama de corpo livre usando o método das juntas para cada junta, no qual sejam indicadas todas as forças atuando no respectivo membro.
Para esse caso não é necessário realizar a análise de todos os membros presentes, sendo possível fazer praticamente apenas a análise das juntas e por elas conterem todas as forças agindo sobre ambas.
Ao final, as forças dependentes de serão comparadas aos valores máximos de tração e compressão suportados pela treliça de acordo com o seu caráter trativo ou compressivo a fim de determinar a força desejada.
Passo 2
Então, escolhendo a junta primeiro e fazendo o seu DCL, tem-se que:
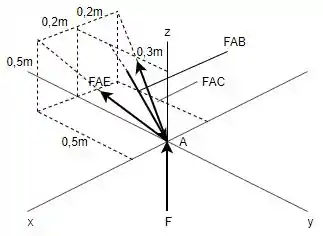
Portanto, a partir destas informações tem-se que para o eixo :
Para o eixo :
E para o eixo :
Passo 3
Então, como as equações , e formam um sistema de três equações com três variáveis é possível resolver e encontrar o valor das forças que serão a solução. Logo, obtém-se:
Como a força age sobre a junta, então possui caráter compressivo.
Já as forças e agem sobre os seus respectivos membros e, logo, possuem caráter trativo.
Passo 4
Agora, fazendo o mesmo processo para a junta :
Com isso, é possível montar as equações do equilíbrio de forças para cada eixo.
Então, para o eixo será feito:
Em seguida, para o eixo :
E para o eixo :
Como as forças e agem sobre seus respectivos membros, então possuem caráter trativo.
Já a força possui caráter compressivo por atuar sobre a junta.
Passo 5
Para finalizar, deve-se determinar o valor de . A fim de realizar isso, os maiores valores de compressão e tração determinados através das análises das juntas devem ser comparados com os valores suportados pela treliça.
Logo, como para compressão o maior valor encontrado é de , tem-se que o valor suportado pela treliça será de:
E para tração será de:
Neste caso, o menor valor obtido irá limitar o valor da força suportada e, portanto, será o valor desejado.