Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 2
A treliça usada para sustentar um balcão está sujeita às cargas mostradas. Considere cada nó como um pino e determine a força em cada membro. Indique se os membros estão sob tração ou compressão. Faça , .
Passo 1
Fala!
O problema quer que a gente encontre a força de cada treliça mostrando se ele está sendo tracionada ou comprimida.
Vamos começar já dando uma olhada na junta . Sabemos que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.
Note que e são as únicas em e só exercem força sob o eixo , portanto eles têm que se anular, então são iguais e sentidos opostos, logo:
(Compressão)
Uma forma de ver que é compressão é repara que está para baixo, comprimindo o segmento .
Note também que então , já que só essas atuam em e somente em . Aí também precisam se anular.
Vamos seguir!
Passo 2
Agora, vamos analisar as forças da junta . Sabemos que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.
No eixo primeiro:
Assim encontramos:
Que por fazer uma força entrando na seção da nossa barrinha, está sob compressão.
Agora no eixo :
Então encontramos:
Como deu negativo, significa que nossa força está no sentido oposto ao da figura, saindo da seção da barrinha. Então temos tração.
Lembre que no passo 1 a gente descobriu que: ? Agora é útil.
Ela também vai ser de tração.
Passo 3
Vamos agora para a junta D.
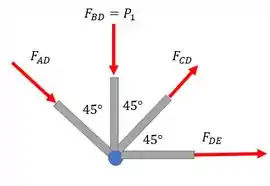
No eixo
Assim encontramos:
Estando ela em tração, saindo da barrinha.
Agora no eixo :
Então encontramos:
O sinal indica que está no sentido contrário ao da imagem. Que nesse caso, por fazer uma força de reação nesse sentido, está sob compressão.
Resposta
(Compressão)
(Compressão)
(Tração)
(Tração)
(Compressão)