Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 61
Determine a intensidade e os ângulos de direção coordenados da força resultante que atua sobre o suporte.
Passo 1
Fala ai galerinha do RespondeAí, tudo beleza? Nesse exercício aqui o enunciado nos fornece duas forças e que atuam sobre um suporte como na figura abaixo:
E com essas informações, o enunciado nos pede para encontrar a intensidade e os ângulos de direção coordenados da força resultante.
Passo 2
Iradoso, a primeira coisa que devemos fazer então é escrever as forças e em termos dos vetores unitários pra podermos somar suas componentes em cada eixo. Bora lá!
Para podemos usar os dois ângulos para escrever as componentes:
Tal que:
Passo 3
Já para temos:
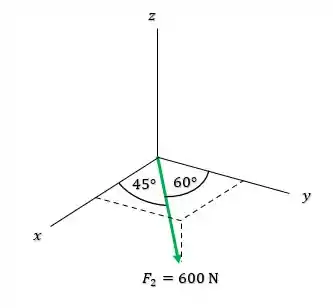
E podemos encontrar as componentes e tal que:
E:
Agora para a componentes precisamos do ângulo entre e o eixo :
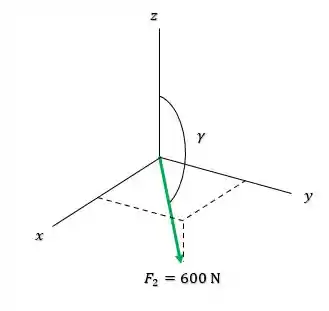
E pra encontrar esse ângulo podemos lembrar da relação:
Logo:
E como a componente está na parte negativa do eixo vamos ter que:
De modo que a força em termos dos vetores unitários será escrita como:
Passo 4
Belezoca, agora que a gente já sabe os valores de e podemos encontrar a força resultante dada como:
Logo:
Somando apenas coordenada com coordenada (o mesmo para as outras coordenadas), temos:
Agora que temos o vetor resultante, para calcularmos a intensidade de um vetor, é só a gente calcular seu módulo, que fica o seguinte:
Passo 5
Show de bolinhas, agora para determinar os ângulos do vetor resultante, aplicarmos a seguinte relação:
Aplicando a inversa do cosseno e substituindo os respectivos valores, vamos obter que: