Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 95
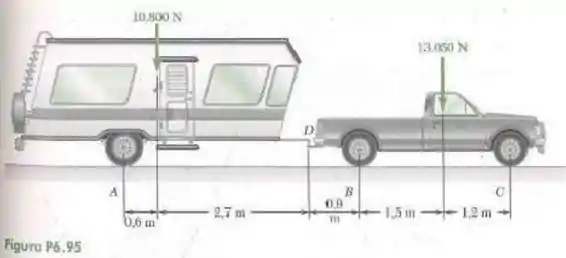
95- O trailer pesa e é rebocado a uma caminhonete de carga de por meio de um engate de rótula fixo em . Determine as reações em cada uma das seis rodas quando a caminhonete e o trailer estão em repouso, o carregamento adicional em cada roda da caminhonete devido ao trailer.
Passo 1
Vamos isolar o trailer da caminhonete e calcular as forças sobre ela:
Note que em temos duas rodas, logo se quisermos calcular a reação em cada roda vamos fazer .
está para cima pois o trailer sem contato nenhum nessa região tenderá a descer, então temos que ter uma força para cima para ele descer.
Calculando a somatória dos momentos em nós temos:
E pela somatória das forças temos que vale:
Na letra não estará no carro e sim em um apoio qualquer, mas vamos guardar esse valor para usar na letra mais tarde
Passo 2
Vamos desenhar o carro em repouso sem influência do trailer.
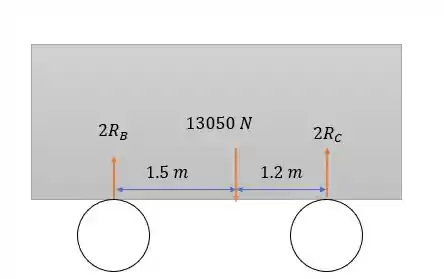
Muito bonito o carro né!
Assim como no trailer, temos duas rodas em e em . Fazendo o momento em temos:
E com isso será pela somatória das forças:
Passo 3
Agora vamos aplicar o peso a influência do trailer em (no sentido contrário a que foi feito no passo anterior, por conta da ação e reação).
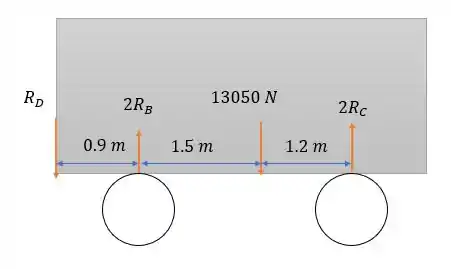
Do passo encontramos:
Logo se fizermos a somatória dos momentos em nós encontraremos:
O que nos dá uma diferença de:
E pela somatória das forças nós encontramos:
Uma diferença de: