Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 19
Um tubo de de diâmetro é apoiado a cada por uma pequena estrutura constituída de dois elementos, tal como mostra a figura. Sabendo que o peso combinado do tubo e seu conteúdo é e desprezando o efeito do atrito, determine a intensidade e a localização do momento fletor máximo no elemento .
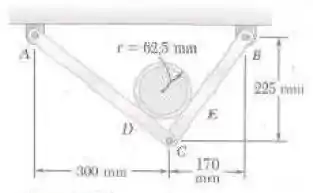
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Para começar, vamos às analises dos apoios:
Temos também que:
Passo 2
Agora, vamos analisar a estrutura:
E:
Somatório de forças em :
Passo 3
Podemos aplicar o momento em para descobrir e consequentemente :
Logo:
Com as reações de , podemos analisar a barra de até :
Logo, o momento máximo é dado por:
Resposta
Exercícios de Livros Relacionados
3.40. A mola tem uma rigidez k = 800 N m e um comprimento não deformado de 200m m . Determine a força nos cabo BC e BD quando a mola é mantida na posição mostrada.
3.41. Um cabo continuo de comprimento total 4m é passado ao redor das pequenas polias em A, B, C e D. Se cada corda está alongada em 300m m , determine a massa m de cada bloco. Despreze o peso das pol
3.26. Determine as trações desenvolvidas nos fios CD, CB e BA e o ângulo θ necessário para o equilíbrio do cilindro E de 15k g e do cilindro F de 30k g .
3.27. Se o cilindro E pesa 150N e θ = 15 ° , determine o peso do cilindro F.
5.49. Determine a intensidade e direção θ da força P mínima necessária para puxar o cilindro de 50k g pelo degrau liso.